已知两同心圆的圆心为O,过小圆上一点M作小圆的弦MA和大圆的弦BMC,且MA⊥BC,求证:AB2+BC2+CA2为定值.
分析:如图,首先根据题意画出图形,过O点作BC垂线,设垂足为D;作MA垂线,设垂足为E,设MB=a,MC=b,MA=c,由Rt△ODC和Rt△OME,推出方程组:
| | [(a+b)]2+()2=R2① | | [(b-a)]2+()2=r2② |
| |
,然后,把a
2+b
2+c
2和2ab分别看做两个整体,通过解方程组求出a
2+b
2+c
2和2ab的值,最后通过等量代换即可推出AB
2+AC
2+BC
2=6R
2+2r
2,为定值.
解答: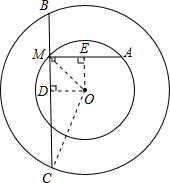
证明:过O点作BC垂线,设垂足为D;作MA垂线,设垂足为E,
设MB=a,MC=b,MA=c,大圆的半径为R,小圆的半径为r,
∵MA⊥BC,
∴AB
2+AC
2+BC
2=(a
2+c
2)+(a
2+b
2)+(a+b)
2=2(a
2+b
2+c
2)+2ab,
∵OD⊥BC,OE⊥MA,
∴CD=
(a+b),ME=
,
∴在Rt△ODC中,[
(a+b)]
2+(
)
2=R
2,
在Rt△OME中,[
(b-a)]
2+(
)
2=r
2,
∴求得方程组:
| | [(a+b)]2+()2=R2① | | [(b-a)]2+()2=r2② |
| |
解方程组的得:
| | a2+b2+c2=2R2+ 2r2 | | 2ab=2R2-2r2 |
| |
,
∴AB
2+AC
2+BC
2=2(a
2+b
2+c
2)+2ab=2(2R
2+2r
2)+2R
2-2r
2=6R
2+2r
2,
∴AB
2+BC
2+CA
2为定值.
点评:本题主要考查勾股定理、垂径定理,关键在于熟练运用相关的性质定理,推出AB2+AC2+BC2=2(a2+b2+c2)+2ab,推出关于a2+b2+c2和2ab的方程组,解方程即可,正确地进行等量代换.

 证明:过O点作BC垂线,设垂足为D;作MA垂线,设垂足为E,
证明:过O点作BC垂线,设垂足为D;作MA垂线,设垂足为E,

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案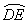 的度数为110°,则
的度数为110°,则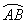 的度数为
的度数为