
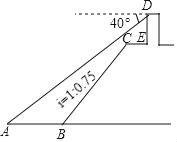
【题目】如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
【答案】5.1.
【解析】
延长DE交AB延长线于点P,作CQ⊥AP,可得CE=PQ=2、CQ=PE,由i=![]() ,可设CQ=4
,可设CQ=4![]() 、BQ=3
、BQ=3![]() ,根据
,根据![]() 求得
求得![]() 的值,即可知DP=11,由AP=
的值,即可知DP=11,由AP=![]() ,结合AB=APBQPQ可得答案.
,结合AB=APBQPQ可得答案.
解:如图,延长DE交AB延长线于点P,作CQ⊥AP于点Q,
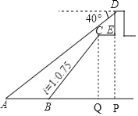
∵CE∥AP,
∴DP⊥AP,
∴四边形CEPQ为矩形,
∴CE=PQ=2(米),CQ=PE,
∵i=![]() ,
,
∴设CQ=4x、BQ=3x,
由BQ2+CQ2=BC2可得(4x)2+(3x)2=102,
解得:x=2或x=﹣2(舍),
则CQ=PE=8(米),BQ=6(米),
∴DP=DE+PE=11(米),
在Rt△ADP中,∵AP=![]() (米),
(米),
∴AB=AP﹣BQ﹣PQ=13.1﹣6﹣2=5.1(米).


科目:初中数学 来源: 题型:
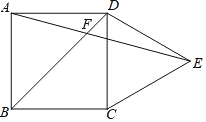
【题目】如图,正方形ABCD,将边CD绕点C顺时针旋转60°,得到线段CE,连接DE,AE,BD交于点F.
(1)求∠AFB的度数;
(2)求证:BF=EF;
(3)连接CF,直接用等式表示线段AB,CF,EF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空:如图,我们知道,一条线段OA绕着它的一个端点O旋转一周,另一个端点所形成的图形叫做 ;一个矩形ABCD绕着它的边AB旋转一周所形成的图形叫做 ;
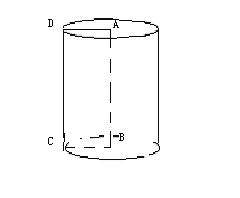
(2)如图,将一个直角三角形ABC(∠C=900)绕着它的直角边AC旋转一周,也能形成一个几何图形。
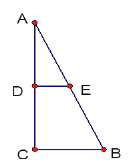
(a)在图中画出这个旋转图形的草图,并说出它的名称。
(b)如果ΔABC中AC=20,BC=15,把这个旋转图形沿着ΔABC的中位线DE且垂直于AC的方向横截,得到一个什么样的图形?并请你计算所截图形的上半部分的全面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数![]() (
(![]() 为常数,且
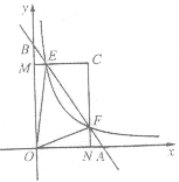
为常数,且![]() )在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若![]() (
(![]() 为大于l的常数).记△CEF的面积为
为大于l的常数).记△CEF的面积为![]() ,△OEF的面积为
,△OEF的面积为![]() ,则
,则![]() =________. (用含
=________. (用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
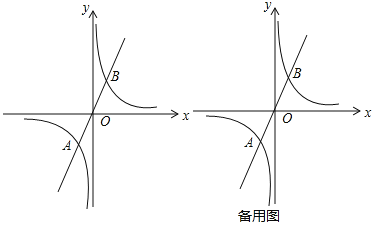
【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数![]() 与
与![]() 的图象性质
的图象性质![]() 小明根据学习函数的经验,对这两个函数当
小明根据学习函数的经验,对这两个函数当![]() 时的图象性质进行了探究
时的图象性质进行了探究![]() 设函数
设函数![]() 与
与![]() 图象的交点为A、
图象的交点为A、![]() 下面是小明的探究过程:
下面是小明的探究过程:
(1)如图所示,若已知A的坐标为![]() ,则B点的坐标为______.
,则B点的坐标为______.
(2)若A的坐标为![]() ,P点为第一象限内双曲线上不同于点B的任意一点.
,P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点![]() 求证:
求证:![]() .
.
证明过程如下:设![]() ,直线PA的解析式为
,直线PA的解析式为![]() .
.
则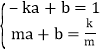
解得![]()
所以,直线PA的解析式为______.
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为![]() 时,判断
时,判断![]() 的形状,并用k表示出
的形状,并用k表示出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
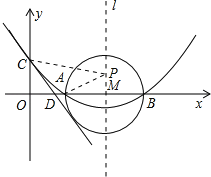
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)在以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
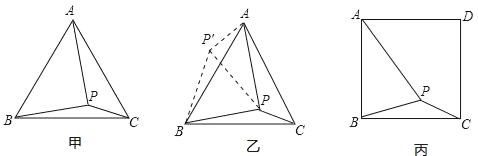
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com