
【题目】足球世界杯预选赛实行主客场的循环赛,即每两支球队都要在自己的主场和客场踢一场.共举行比赛![]() 场,则参加比赛的球队共有________支.
场,则参加比赛的球队共有________支.
【答案】15
【解析】
设参加比赛的球队共有x支,则每支球队都要与余下的(x-1)支球队进行比赛,又每两支球队都要在自己的主场和客场踢一场,即每两支球队相互之间都要比赛两场,故这x支球队一共需要比赛x(x-1)场,而这个场次又是210场,据此列出方程.
解:设参加比赛的球队共有x支,每一个球队都与剩余的x-1队打球,即共打x(x-1)场,
∵每两支球队都要在自己的主场和客场踢一场,即每两支球队相互之间都要比赛两场,
∴每两支球队相互之间都要比赛两场,
即x(x-1)=210,
解得:x2-x-210=0,
(x-15)(x+14)=0,
x1=15.x2=-14(负值舍去)
故参加比赛的球队共有15支.
故答案为:15


科目:初中数学 来源: 题型:
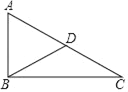
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线.
(1)按如下要求尺规作图,保留作图痕迹,标注相应的字母:过点C作直线CE,使CE⊥BC于点C,交BD的延长线于点E,连接AE;
(2)求证:四边形ABCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)~(2)题:
数学课上,老师出示了一道题:如图1,将一个直角三角板![]() 的直角边
的直角边![]() 摆放在直线
摆放在直线![]() 上,然后以直角顶点
上,然后以直角顶点![]() 为旋转中心顺时针旋转这个三角板.若射线
为旋转中心顺时针旋转这个三角板.若射线![]() 平分
平分![]() 、探究
、探究![]() 和
和![]() 的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
的数量关系,并说明经过一段时间的思考后,同学们开始了交流:
小明:我根据老师的叙述画出图2,并计算出当![]() 时,
时,![]() 的度数是
的度数是![]() ;
;
小红:在小明的图形中,点![]() 、
、![]() 都在
都在![]() 的上方,我发现,在这种情况下,
的上方,我发现,在这种情况下,![]() 始终在
始终在![]() 的内部.若设
的内部.若设![]() 的度数是
的度数是![]() ,通过计算,
,通过计算,![]() 的度数可以用含
的度数可以用含![]() 的式子表示,得到
的式子表示,得到![]() 和
和![]() 的数量关系是
的数量关系是![]() ;
;
小华:我除了画小明的这种图形,还画了其余几种,也分别得出![]() 和
和![]() 的数量关系,从而解决了老师提出的问题.
的数量关系,从而解决了老师提出的问题.
老师:这些同学都先画出图形,再解决问题,这体现了图形的直性,但要注意一点,在初中阶段我们研究的角都是小于![]() 的.随着大家交流的深入,点
的.随着大家交流的深入,点![]() 的位置由
的位置由![]() 上方到直线
上方到直线![]() 外,
外,![]() 的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
的值由数字到字母,这体现了从特殊到一般的思想,同学们再根据小华所说的进行探究,还能归纳出其他的数学思想方法!
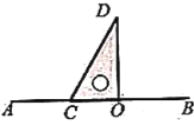
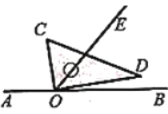
图1 图2
(1)如图2,点![]() 、
、![]() 都在
都在![]() 上方,
上方,![]() .
.
①用含![]() 的代数式表示
的代数式表示![]() 为_____________;
为_____________;
②小红的“![]() 始终在
始终在![]() 的内部”的说法是正确的吗,为什么?
的内部”的说法是正确的吗,为什么?
(2)根据小华的叙述,写出![]() 与
与![]() 的数量关系并说明.
的数量关系并说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一系列用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察并解答下列问题:
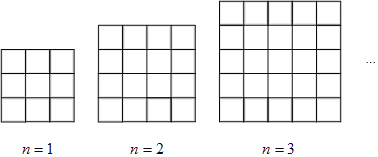
(1)在第n个图形中,共有多少块黑瓷砖(用含n的代数式表示);
(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;
(3)当n=12时,求y的值;
(4)若黑瓷砖每块3元,白瓷砖每块2元,在问题(3)中,试求共需花多少元购买瓷砖.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①![]() 必是负数;②绝对值最小的数是0;③在数轴上,原点两旁的两个点表示的数必互为相反数;④在数轴上,左边的点比右边的点所表示的数大,其中正确的有( )
必是负数;②绝对值最小的数是0;③在数轴上,原点两旁的两个点表示的数必互为相反数;④在数轴上,左边的点比右边的点所表示的数大,其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣8ax+12a(a<0)与x轴交于A、B两点(点A在点B的左边),抛物线上另有一点C在第一象限,且使△OCA∽△OBC,
(1)求OC的长及![]() 的值;
的值;
(2)设直线BC与y轴交于P点,当点C恰好在OP的垂直平分线上时,求直线BP和抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,同时点
的速度移动,同时点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为
的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为![]() 秒,
秒,

![]() 求 秒后,
求 秒后, ![]() 的面积等于
的面积等于![]()
![]() 求 秒后,
求 秒后,![]() 的长度等于
的长度等于![]()
![]() 运动过程中,四边形APQC的面积能否等于
运动过程中,四边形APQC的面积能否等于![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元,已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次采购的数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.为出口需要,所有采购的大蒜必须在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=( )
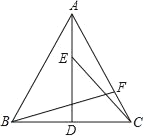
A. 112.5°B. 105°C. 90°D. 82.5°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com