
 24、如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,你能判断BE与AC的位置关系吗?请说明理由.
24、如图,点B在DC上,BE平分∠ABD,∠DBE=∠A,你能判断BE与AC的位置关系吗?请说明理由.科目:初中数学 来源: 题型:阅读理解
| 5 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2011-2012年浙江省温岭市八年级第一学期四校期中联考数学卷 题型:解答题
(13分)阅读下列材料,并回答问题.
画一个直角三角形,使它的两条直角边分别为5和12,那么我们可以量得直角三角形的斜边长为13,并且 。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则
。事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方。如果直角三角形中,两直角边长分别为a、b,斜边长为c,则 ,这个结论就是著名的勾股定理.
,这个结论就是著名的勾股定理.
请利用这个结论,完成下面的活动:
(1)一个直角三角形的两条直角边分别为6、8,那么这个直角三角形斜边长为 .
(2)满足勾股定理方程 的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
的正整数组(a,b,c)叫勾股数组。例如(3,4,5)就是一组勾股数组。观察下列几组勾股数
① 3, 4, 5 ; ② 5,12,13 ; ③ 7,24,25 ;④ 9,40,41 ;
请你写出有以上规律的第⑤组勾股数: .
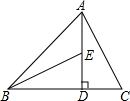
(3)如图,AD⊥BC于D,AD=BD,AC=BE。AC=3,DC=1,求BD的长度.

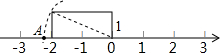
(4)如图,点A在数轴上表示的数是 ,请用类似的方法在下图数轴上画出表示数 的B点(保留作图痕迹).
的B点(保留作图痕迹).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com