
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

【答案】(1)证明见试题解析;(2)![]() .
.
【解析】试题分析:(1)先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CD;
(2)由菱形的性质得到DE=AE=AC=AB=1,AC∥DE,根据等腰三角形的性质得∠AEB=∠ABE,根据平行线得性质得∠ABE=∠BAC=45°,所以∠AEB=∠ABE=45°,于是可判断△ABE为等腰直角三角形,所以BE=![]() AC=
AC=![]() ,于是利用BD=BE﹣DE求解.
,于是利用BD=BE﹣DE求解.
试题解析:(1)∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,∴AE=AB,AF=AC,∠EAF=∠BAC,∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,∵AB=AC,∴AE=AF,∴△AEB可由△AFC绕点A按顺时针方向旋转得到,∴BE=CD;
(2)∵四边形ACDE为菱形,AB=AC=1,∴DE=AE=AC=AB=1,AC∥DE,∴∠AEB=∠ABE,∠ABE=∠BAC=45°,∴∠AEB=∠ABE=45°,∴△ABE为等腰直角三角形,∴BE=![]() AC=
AC=![]() ,∴BD=BE﹣DE=
,∴BD=BE﹣DE=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下面给出四边形ABCD中,∠A , ∠B , ∠C , ∠D的度数之比,其中能判定四边形ABCD为平行四边形的是( )
A.1∶2∶3∶4
B.2∶3∶2∶3
C.2∶2∶3∶3
D.1∶2∶2∶3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当两条直线相交所成的四个角中_________,叫做这两条直线互相垂直,其中的一条直线叫_________,它们的交点叫_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国最长的河流长江全长约为6300千米,数6300用科学记数法表示为( )
A. 0.63×104 B. 6.3×103 C. 63×102 D. 6.3×106
查看答案和解析>>
科目:初中数学 来源: 题型:
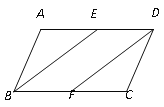
【题目】如图, 在□ABCD中,点E、F是AD、BC的中点,连接BE、DF.
(1)求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,AB=6cm,BC=10cm,试求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借助表格进行多项式乘多项式运算,可以方便合并同类项得出结果,下面尝试利用表格试一试:
例题:(a+b)(a-b)
解:填表

则(a+b)(a-b)=a2-b2.
根据所学完成下列问题:
(1)如表,填表计算(x+2)(x2-2x+4),(m+3)(m2-3m+9),直接写出结果.


结果为 ; 结果为
(2)根据以上获得的经验填表:

结果为 △3 + ○3,根据以上探索,请用字母a、b来表示发现的公式为 .
(3)用公式计算:(2x+3y)(4x2-6xy+9y2)= ;
因式分解:27m3-8n3= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com