
【题目】如图,在平行四边形ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
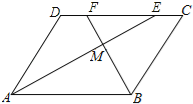
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
【答案】(1)证明见解析;(2)DF=CE,理由见解析.
【解析】试题分析:(1)利用平行四边形的性质得到AD∥BC,然后得到∠DAB+∠ABC=180°,然后根据角的平分线得出∠DAB=2∠BAE,∠ABC=2∠ABF,等量代换得出∠BAE+∠ABF=90°即可;(2)先猜想DF=CE,利用角的平分线和平行线的性质可得DE=AD,CF=BC,然后利用线段的和差关系可得出结论.
试题解析:(1)∵在平行四边形ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分别平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF.
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
(2)DF=CE,
∵在平行四边形ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.∴∠DEA=∠DAE.
∴DE=AD.
同理可得,CF=BC.
又∵在平行四边形ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.


科目:初中数学 来源: 题型:
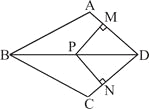
【题目】在四边形ABCD中,AB=BC,对角线BD平分![]() ,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.
,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.
(1)求证: ![]() ;
;
(2)若![]() ,求证:四边形MPND是正方形。
,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图(1)所示,若DF⊥AC,垂足为F,AB=4,求BE的长;
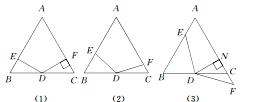
(2)如图(2)所示,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F,求证:BE+CF=![]() AB;
AB;
(3)如图(3)所示,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交于点F,作DN⊥AC于点N,若DN=FN,求证:BE+CF=![]() (BE-CF).
(BE-CF).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程4x2=5x+2化为一般形式后的二次项、一次项、常数项分别是( )
A. 4x2, 5x, 2 B. -4x2, -5x, -2
C. 4x 2 , -5x,, -2 D. 4x2, -5x, 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.

(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com