
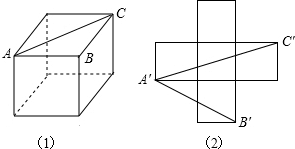
分析 (1)由长方形中最长的线段为对角线,从而可根据已知运用勾股定理求得最长线段的长;
(2)要确定角的大小关系,一般把两个角分别放在两个三角形中,然后根据三角形的特点或者全等或者相似形来解.
解答 解:(1)如图(1)中的A′C′,在Rt△A′C′D′中,∵C′D′=1,A′D′=3,由勾股定理得,
∴$A'C'=\sqrt{C'D{'}^{2}+A'D{'}^{2}}=\sqrt{10}$
(2)∵立体图中∠BAC为平面等腰直角三角形的一锐角,
∴∠BAC=45°.
在平面展开图中,连接线段B′C′,由勾股定理可得:A'B'=$\sqrt{5}$,B'C'=$\sqrt{5}$.
又∵A′B′2+B′C′2=A′C′2,
由勾股定理的逆定理可得△A'B'C'为直角三角形.
又∵A′B′=B′C′,
∴△A′B′C′为等腰直角三角形.
∴∠B′A′C′=45°.
∴∠BAC与∠B′A′C′相等.
点评 本题综合考查了展开与折叠,等腰直角三角形,勾股定理的知识,是一道综合性比较强的题,难度中等.


科目:初中数学 来源: 题型:解答题
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车装载量/吨 | 6 | 5 | 4 |
| 每吨所需运费/元/吨 | 120 | 160 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
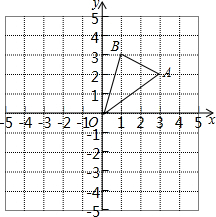 如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
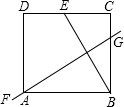 如图,在矩形纸片ABCD中,点E是DC的中点,BE的垂直平分线FG恰好经过点A,则$\frac{BC}{AB}$=( )
如图,在矩形纸片ABCD中,点E是DC的中点,BE的垂直平分线FG恰好经过点A,则$\frac{BC}{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9000}{x+3000}=\frac{15000}{x}$ | B. | $\frac{9000}{x}=\frac{15000}{x-3000}$ | ||
| C. | $\frac{9000}{x}=\frac{15000}{x+3000}$ | D. | $\frac{9000}{x-3000}=\frac{15000}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com