
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=12,AB=16,求菱形ADCF的面积.
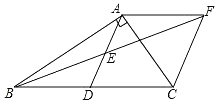
【答案】(1)详见解析;(2)96.
【解析】
(1)先证明△AEF≌△DEB(AAS),得AF=DB,根据一组对边平行且相等可得四边形ADCF是平行四边形,由直角三角形斜边中线的性质得:AD=CD,根据菱形的判定即可证明四边形ADCF是菱形;
(2)先根据菱形和三角形的面积可得:菱形ADCF的面积=直角三角形ABC的面积,即可解答.
解:(1)证明:∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AEF和△DEB中,
∵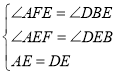 ,
,
∴△AEF≌△DEB(AAS),
∴AF=DB,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=CD=![]() BC,
BC,
∴四边形ADCF是菱形;
(2)解:设AF到CD的距离为h,
∵AF∥BC,AF=BD=CD,∠BAC=90°,
∴S菱形ADCF=CDh=![]() BCh=S△ABC=
BCh=S△ABC=![]() ABAC=
ABAC=![]() ×12×16=96.
×12×16=96.


科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2016次,点B的落点依次为B1,B2,B3,…,则B2016的坐标为_________.
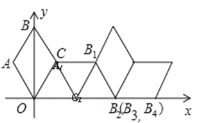
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+4与抛物线y=﹣![]() x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;
(3)点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
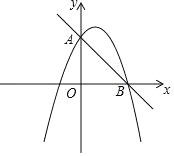
查看答案和解析>>
科目:初中数学 来源: 题型:
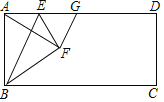
【题目】如图,在矩形![]() 中,点
中,点![]() 是
是![]() 上的一个动点,连结
上的一个动点,连结![]() ,作点
,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,且点
,且点![]() 落在矩形
落在矩形![]() 的内部,连结
的内部,连结![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,设
,设![]() ,
,
(1)求证:![]() ;
;
(2)当点![]() 落在
落在![]() 上时,用含
上时,用含![]() 的代数式表示
的代数式表示![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
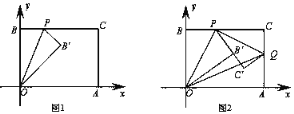
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
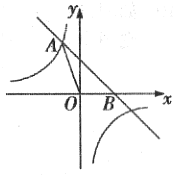
【题目】如图,直线y=﹣x+2与反比例函数y=![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)写出直线y=﹣x+2向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
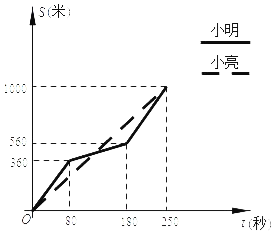
【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次男子1000米耐力测试中,小明和小亮同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示:
(1)当80≤t≤180时,求小明所跑的路程S(米)与所用的时间t(秒)之间的函数表达式;
(2)求他们第一次相遇的时间是起跑后的第几秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com