
【题目】先阅读下面的知识,后解答后面的问题:
探究:如图,在△ABC中,已知∠B=∠C,求证:AB=AC.

证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C, , , 所以△ABD≌△ACD( ),所以AB=AC.
(1)完成上述证明中的空白;
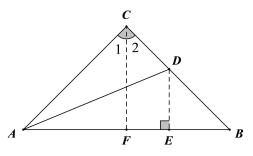
(2)已知如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB.试问:AC+CD与AB相等吗?说明理由.

【答案】(1)![]() ,AD=AD,AAS;(2)AC+CD=AB,理由见解析.
,AD=AD,AAS;(2)AC+CD=AB,理由见解析.
【解析】
(1)根据AAS可判定△ABD≌△ACD,进而完成填空;
(2)过点D作DE⊥AB,垂足为E,如图,先用AAS证明△ACD≌△AED,得到AC=AE,再作∠ACB的平分线CF交AB于点F,利用SAS证明△ACF≌△BCF,得到∠CAB=∠B,进一步通过三角形的内角和得出∠DEB=∠B,进而根据探究结论推出ED=EB,即可证得结论.
解:(1)证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C,![]() , AD=AD ,
, AD=AD ,
所以△ABD≌△ACD(AAS),
所以AB=AC.
故答案为:![]() ,AD=AD,AAS.
,AD=AD,AAS.
(2)AC+CD=AB,理由如下:
过点D作DE⊥AB,垂足为E,如图,则∠AED=90°,
∵∠ACB=90°,∴∠ACB=∠AED,
∵AD平分∠CAB,∴∠CAD=∠EAD,
在△ACD和△AED中,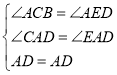
∴△ACD≌△AED(AAS).
∴AC=AE,CD=ED,
作∠ACB的平分线CF交AB于点F,则∠1=∠2,
在△ACF和△BCF中,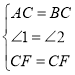
∴△ACF≌△BCF(SAS),∴∠CAB=∠B,
∵∠ACB=90°,∴∠CAB=∠B=45°,
∴∠DEB=90°-∠B=45°,
∴∠DEB=∠B,
由探究结论知:ED=EB.
∴BE=CD,
∴AB=AE+BE=AC+CD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一般情况下,对于数![]() 和
和![]() ,
,![]() (≠,不等号),但是对于某些特殊的数
(≠,不等号),但是对于某些特殊的数![]() 和
和![]() ,
,![]() 我们把这些特殊的数
我们把这些特殊的数![]() 和
和![]() ,称为“理想数对”,记作
,称为“理想数对”,记作![]() .例如当
.例如当![]() 时,有
时,有![]() ,那么
,那么![]() 就是“理想数对”.
就是“理想数对”.
(1)![]() 可以称为“理想数对”的是 ;
可以称为“理想数对”的是 ;
(2)如果![]() 是“理想数对”,那么
是“理想数对”,那么![]() = ;
= ;
(3)若![]() 是“理想数对”,求
是“理想数对”,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面一列数,探究其中的规律:—1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)填空:第11,12,13三个数分别是 , , ;
(2)第2020个数是什么?
(3)如果这列数无限排列下去,与哪个数越来越近?
查看答案和解析>>
科目:初中数学 来源: 题型:
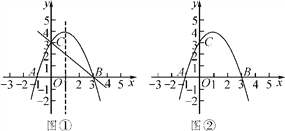
【题目】抛物线y=-x2+2x+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)抛物线的对称轴上存在点P,使∠APB=∠ABC,利用图①求点P的坐标;
(3)点Q在y轴右侧的抛物线上,利用图②比较∠OCQ与∠OCA的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
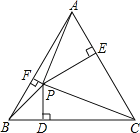
【题目】如图,P为边长为2的等边三角形ABC内任意一点,连接PA、PB、PC,过P点分别作BC、AC、AB边的垂线,垂足分别为D、E、F,则PD+PE+PF等于( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过反比例函数![]() (
(![]() )图像上一动点M作MN⊥x轴交x轴于点N,Q是直线MN上一点,且MQ=2MN,过点Q作QR∥
)图像上一动点M作MN⊥x轴交x轴于点N,Q是直线MN上一点,且MQ=2MN,过点Q作QR∥![]() 轴交该反比例函数图像于点R,已知S△QRM=8,那么k的值为_____.
轴交该反比例函数图像于点R,已知S△QRM=8,那么k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
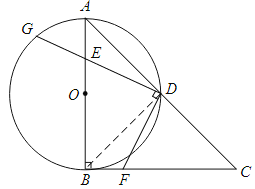
【题目】如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.
(1)求证:AE=BF;
(2)连接EF,求证:∠FEB=∠GDA;
(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.
(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com