
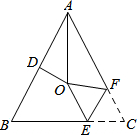
 如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )| A. | 106° | B. | 108° | C. | 110° | D. | 112° |
分析 连接OB、OC,根据角平分线的定义求出∠BAO,根据等腰三角形两底角相等求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB,根据等边对等角可得∠ABO=∠BAO,再求出∠OBC,然后判断出点O是△ABC的外心,根据三角形外心的性质可得OB=OC,再根据等边对等角求出∠OCB=∠OBC,根据翻折的性质可得OE=CE,然后根据等边对等角求出∠COE,再利用三角形的内角和定理列式计算即可得解.
解答 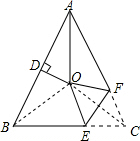 解:如图,连接OB、OC,
解:如图,连接OB、OC,
∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×54°=27°,
又∵AB=AC,
∴∠ABC=$\frac{1}{2}$(180°-∠BAC)=$\frac{1}{2}$(180°-54°)=63°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°-27°=36°,
∵AO为∠BAC的平分线,AB=AC,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线,
∴点O是△ABC的外心,
∴∠OCB=∠OBC=36°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°,
故选B.
点评 本题考查了翻折变换的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形三线合一的性质,等边对等角的性质,综合性较强,难度较大,作辅助线,构造出等腰三角形是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
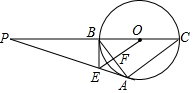 如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.
如图,△ABC内接于⊙O,BC是直径,⊙O的切线PA交CB的延长线于点P,OE∥AC交AB于点F,交PA于点E,连接BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com