
如图1,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.
(1)当t= 时,△PQR的边QR经过点B;
(2)设△PQR和矩形OABC重叠部分的面积为S,求S关于t的函数关系式;
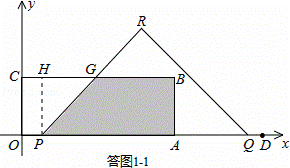
(3)如图2,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,求t的值.
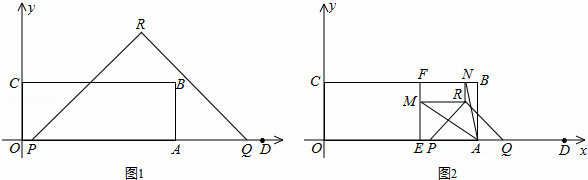
解:(1)△PQR的边QR经过点B时,△ABQ构成等腰直角三角形,
∴AB=AQ,即3=4﹣t,
∴t=1.
即当t=1秒时,△PQR的边QR经过点B.
(2)①当0≤t≤1时,如答图1﹣1所示.
设PR交BC于点G,
过点P作PH⊥BC于点H,则CH=OP=2t,GH=PH=3.
S=S矩形OABC﹣S梯形OPGC
=8×3﹣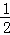 (2t+2t+3)×3
(2t+2t+3)×3
=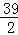 ﹣6t;
﹣6t;
②当1<t≤2时,如答图1﹣2所示.
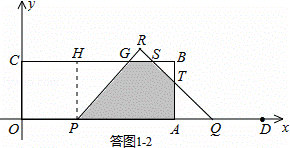
设PR交BC于点G,RQ交BC、AB于点S、T.
过点P作PH⊥BC于点H,则CH=OP=2t,GH=PH=3.
QD=t,则AQ=AT=4﹣t,
∴BT=BS=AB﹣AQ=3﹣(4﹣t)=t﹣1.
S=S矩形OABC﹣S梯形OPGC﹣S△BST
=8×3﹣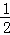 (2t+2t+3)×3﹣
(2t+2t+3)×3﹣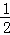 (t﹣1)2
(t﹣1)2
=﹣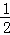 t2﹣5t+19;
t2﹣5t+19;
③当2<t≤4时,如答图1﹣3所示.
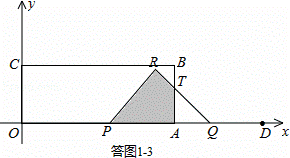
设RQ与AB交于点T,则AT=AQ=4﹣t.
PQ=12﹣3t,∴PR=RQ=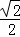 (12﹣3t).
(12﹣3t).
S=S△PQR﹣S△AQT
=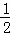 PR2﹣
PR2﹣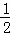 AQ2
AQ2
=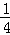 (12﹣3t)2﹣
(12﹣3t)2﹣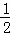 (4﹣t)2
(4﹣t)2
=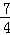 t2﹣14t+28.
t2﹣14t+28.
综上所述,S关于t的函数关系式为:
S=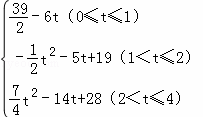 .
.
(3)∵E(5,0),∴AE=AB=3,
∴四边形ABFE是正方形.
如答图2,将△AME绕点A顺时针旋转90°,得到△ABM′,其中AE与AB重合.
∵∠MAN=45°,∴∠EAM+∠NAB=45°,
∴∠BAM′+∠NAB=45°,
∴∠MAN=∠M′AN.
连接MN.在△MAN与△M′AN中,
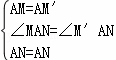
∴△MAN≌△M′AN(SAS).
∴MN=M′N=M′B+BN
∴MN=EM+BN.
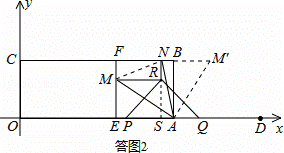
设EM=m,BN=n,则FM=3﹣m,FN=3﹣n.
在Rt△FMN中,由勾股定理得:FM2+FN2=MN2,即(3﹣m)2+(3﹣n)2=(m+n)2,
整理得:mn+3(m+n)﹣9=0. ①
延长MR交x轴于点S,则m=EM=RS=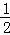 PQ=
PQ=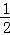 (12﹣3t),
(12﹣3t),
∵QS=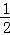 PQ=
PQ=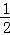 (12﹣3t),AQ=4﹣t,
(12﹣3t),AQ=4﹣t,
∴n=BN=AS=QS﹣AQ=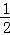 (12﹣3t)﹣(4﹣t)=2﹣
(12﹣3t)﹣(4﹣t)=2﹣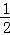 t.
t.
∴m=3n,
代入①式,化简得:n2+4n﹣3=0,
解得n=﹣2+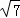 或n=﹣2﹣
或n=﹣2﹣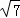 (舍去)
(舍去)
∴2﹣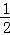 t=﹣2+
t=﹣2+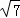
解得:t=8﹣2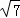 .
.
∴若∠MAN=45°,则t的值为(8﹣2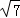 )秒
)秒


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进 、
、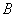 两种型号的低排量汽车,其中
两种型号的低排量汽车,其中 型汽车的进货单价比
型汽车的进货单价比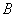 型汽车的进货单价多2万元;花50万元购进
型汽车的进货单价多2万元;花50万元购进 型汽车的数量与花40万元购进
型汽车的数量与花40万元购进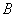 型汽车的数量相同.销售中发现
型汽车的数量相同.销售中发现 型汽车的每周销量
型汽车的每周销量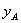 (台)与售价
(台)与售价 (万元/台)满足函数关系
(万元/台)满足函数关系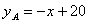 ,
,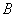 型汽车的每周销量
型汽车的每周销量 (台)与售价
(台)与售价 (万元/台)满足函数关系
(万元/台)满足函数关系
(1)求 、
、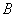 两种型号的汽车的进货单价;
两种型号的汽车的进货单价;
(2)已知 型汽车的售价比
型汽车的售价比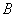 型汽车的售价高2万元/台.设
型汽车的售价高2万元/台.设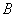 型汽车售价为
型汽车售价为 万元/台,每周销售这两种车的总利润为
万元/台,每周销售这两种车的总利润为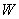 万元,求
万元,求 与
与 的函数关系式,
的函数关系式,  、
、 两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
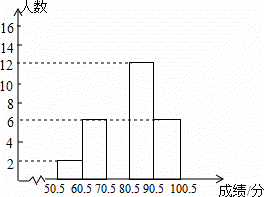
某公司为了解员工对“六五”普法知识的知晓情况,从本公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
| 组别 | 分数段/分 | 频数/人数 | 频率 |
| 1 | 50.5~60.5 | 2 | a |
| 2 | 60.5~70.5 | 6 | 0.15 |
| 3 | 70.5~80.5 | b | c |
| 4 | 80.5~90.5 | 12 | 0.30 |
| 5 | 90.5~100.5 | 6 | 0.15 |
| 合计 | 40 | 1.00 |
(1)表中a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系 中,二次函数
中,二次函数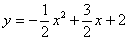 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C.过动点H(0,
轴交于点C.过动点H(0,  )作平行于
)作平行于 轴的直线,直线与二次函数
轴的直线,直线与二次函数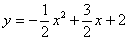 的图像相交于点D,E.
的图像相交于点D,E.
(1)写出点A,点B的坐标;
(2)若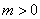 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与 轴相切时,求
轴相切时,求 的值;
的值;
(3)直线上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com