
����Ŀ����ͼ�����κ���y=![]() x2+bx+c��ͼ�����B��0��1����C��4��3�����㣬��x�ύ�ڵ�D����E������B�͵�C��ֱ����x�ύ�ڵ�A��
x2+bx+c��ͼ�����B��0��1����C��4��3�����㣬��x�ύ�ڵ�D����E������B�͵�C��ֱ����x�ύ�ڵ�A��
(1)����κ����Ľ���ʽ��
(2)��x������һ����P�����ŵ�P���ƶ������ڵ�Pʹ��PBC��ֱ�������Σ����������P�����ꣻ
(3)������P��A���������x������x����������ÿ��2����λ���ٶ��˶���ͬʱ����QҲ��A���������ÿ��a����λ���ٶ�������AC�˶����Ƿ������A��P��QΪ���������������ABD���ƣ������ڣ�ֱ��д��a��ֵ���������ڣ�˵�����ɣ�

���𰸡�(1)�����߽���ʽy=![]() x2�C
x2�C![]() x+1��(2)��P������1��0������3��0������
x+1��(2)��P������1��0������3��0������![]() ��0������
��0������![]() ��0����(3)a=
��0����(3)a=![]() ��
��![]() ��
��
��������
(1) ��B��C�������������κ�������ʽ,ͨ����������������b��c��ֵ�����������������ʽ;
(2)��P��x��0�����ɡ�PBC��ֱ�������Σ��֡�CBP=90�����BPC=90������������ۣ����ù��ɶ����ɵ�x��ֵ�������õ�P������;
(3)��������С�APQ�ס�ADB���APQ�ס�ABD,���Ӧ�߳ɱ����������a��ֵ.
(1)�߶��κ���y=0.5x2+bx+c��ͼ�����B��0��1����C��4��3�����㣬
��![]() �����
�����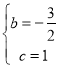 ��
��
�������߽���ʽy=![]() x2�C
x2�C![]() x+1��
x+1��
(2)���P������x��0����
�ߵ�P��x��0������B��0��1������C��4��3����
��PB=![]() =
=![]() ��
��
CP=![]() =
=![]() ��
��
BC=![]() =2
=2![]() ��
��
����BCP=90������BP2=BC2+CP2��
��x2+1=20+x2�C8x+25����x=![]() ��
��
����CBP=90������CP2=BC2+BP2��
��x2+1+20=x2�C8x+25����x=![]() ��
��
����BPC=90������BC2=BP2+CP2��
��x2+1+x2�C8x+25=20��
��x1=1��x2=3��
������������P������1��0������3��0������![]() ��0������
��0������![]() ��0����
��0����
(3)a=![]() ��
��![]() ��
��
�������߽���ʽy=![]() x2�C
x2�C![]() x+1��x�ύ�ڵ�D����E��
x+1��x�ύ�ڵ�D����E��
��0=![]() x2�C
x2�C![]() x+1����x1=1��x2=2�����D��1��0����
x+1����x1=1��x2=2�����D��1��0����
�ߵ�B��0��1����C��4��3����
��ֱ��BC����ʽy=![]() x+1��
x+1��
��y=0ʱ��x=�C2�����A���C2��0����
�ߵ�A���C2��0������B��0��1������D��1��0����
��AD=3��AB=![]() ��
��
�辭��t�룬��AP=2t��AQ=at��
����APQ�ס�ADB��
��![]() ����
����![]() ����a=
����a=![]() ��
��
����APQ�ס�ABD����![]() ����
����![]() ����a=
����a=![]() ��
��
����������a=![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���![]() ͼ���һ���֣��Գ�����ֱ��x=��2.�������н��ۣ���ab<0����
ͼ���һ���֣��Գ�����ֱ��x=��2.�������н��ۣ���ab<0����![]() ����
����![]() ����
����![]() ���ݷ���
���ݷ���![]() ��������Ϊ
��������Ϊ![]() ��
��![]() ������ȷ�Ľ����У� ��
������ȷ�Ľ����У� ��
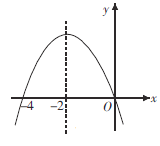
A.�٢ۢ�B.�ڢܢ�C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
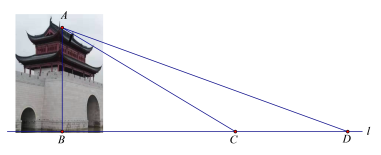
����Ŀ��ˮ����λ�ڵ��ֺӺ���ۺ�����ڣ��ǻ���ˮϵ�����ֺ��ε���������Ҫ�ı�־�Ծ��ۣ��ڿ���ʵ����У�ijУ���꼶��ѧ��ȤС�����������ˮ���ŵĸߣ����ǵIJ����������£���ͼ������D����õ�A������Ϊ20��������ˮ���ŵķ���ǰ��13����C������õ�A������Ϊ31������D��C��B��һֱ���ϣ������ˮ����AB�ĸߣ�����ȷ��0.1�ף�
���ο����ݣ�sin20���0.34��cos20���0.94��tan20���0.36��sin31���0.52��cos31���0.86��tan31���0.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ˮƽ����ƽ��ֱ������ϵ�У���
ˮƽ����ƽ��ֱ������ϵ�У���![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����
����![]() �ں���
�ں���![]() ��ͼ���ϣ�
��ͼ���ϣ�

![]() ����
����![]() �ı���ʽ��
�ı���ʽ��
![]() ���
���![]() �����ꣻ
�����ꣻ
![]() ��
��![]() ��
��![]() ��������ƽ��
��������ƽ��![]() ����λ���жϵ�
����λ���жϵ�![]() �ܷ����ں���
�ܷ����ں���![]() ��ͼ���ϣ���˵�����ɣ�
��ͼ���ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ���������ڡ�����֮�ʣ�ijУ�ٰ����ԡ��ҵ��ഺ��������Ϊ������ݽ������� ���Ӳμӱ�����ѧ���������ȡ����ѧ�����ݽ��ɼ�����ͳ��(�ȼ���A�����㣬B�����ã�C��һ�㣬D���ϲ�)��������������ͳ��ͼ��(������Ϣδ����)��
�ȼ� | ���� |
A | m |
B | 20 |
C | n |
D | 10 |

�����ͳ��ͼ���е���Ϣ����������⣺
(1)��ι���ȡ��________���μ��ݽ�������ѧ����ͳ��ͼ��a��________��b��________��
(2)����Уѧ������2000�ˣ�������μ����ݽ�������������Ƴɼ��ﵽ������ж����ˣ�
(3)���ݽ������ɼ�ΪA�ȼ���ѧ����ǡ����2��Ů���������ѧ��Ϊ��������A�ȼ���ѧ���г�ȡ����ͬѧ�μ�ȫ���ݽ������������һ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
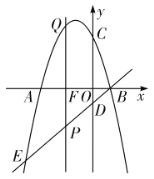
����Ŀ����ͼ���Գ���Ϊֱ��x����2��������y��x2+bx+c��x�ύ��A(��5��0)��B(1��0)���㣬��y���ཻ�ڵ�C��
��1���������ߵĽ���ʽ��������������꣮
��2������P���������ϣ���S��POC��4S��BOC�������P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ��ֱ��
��ֱ��![]() �������߽��ڵ�
�������߽��ڵ�![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
��1���������ߵĽ���ʽ��
��2����![]() ���߶�
���߶�![]() �ϵ�һ���㣨����
�ϵ�һ���㣨����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ��Ĵ��ߣ���
��Ĵ��ߣ���![]() ���ڵ�
���ڵ�![]() �����������ڵ�
�����������ڵ�![]() ����
����![]() ���߶�
���߶�![]() �Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
�Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
��3����![]() ���ϴ���һ��
���ϴ���һ��![]() ��ʹ��
��ʹ��![]() ʱ�������
ʱ�������![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
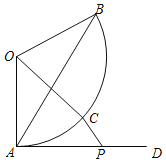
����Ŀ����ͼ��������AOB�У�OA��OB��4����AOB��120�㣬��C�ǻ�AB�ϵ�һ�����㣨�����A��B�غϣ�������AD������AOB���ڡ�O���У���P������AD�ϣ�����AB��OC��CP����AP��2![]() ����CP��ȡֵ��Χ��_____��
����CP��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ֶ�������n����C���������ٵ�nΪ����ʱ�����Ϊ3n+1���ڵ�nΪż��ʱ�����Ϊ![]() ������k��ʹ
������k��ʹ![]() Ϊ�����������������������ظ����У����磬n��66ʱ������C���������£�
Ϊ�����������������������ظ����У����磬n��66ʱ������C���������£�
![]()
��n��26�����2019����C�������Ľ����_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com