
【题目】如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
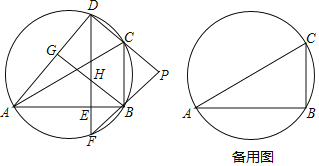
【答案】(1)证明见解析;(2)20°或40°.
【解析】
(1)根据等边对等角得:∠PCB=∠PBC,由四点共圆的性质得:∠BAD+∠BCD=180°,从而得:∠BFD=∠PCB=∠PBC,根据平行线的判定得:BC∥DF,可得∠ABC=90°,AC是⊙O的直径,从而得:∠ADC=∠AGB=90°,根据同位角相等可得结论;
(2)先证明四边形BCDH是平行四边形,得BC=DH,根据特殊的三角函数值得:∠ACB=60°,∠BAC=30°,所以DH=![]() AC,分两种情况:
AC,分两种情况:
①当点O在DE的左侧时,如图2,作辅助线,构建直角三角形,由同弧所对的圆周角相等和互余的性质得:∠AMD=∠ABD,则∠ADM=∠BDE,并由DH=OD,可得结论;
②当点O在DE的右侧时,如图3,同理作辅助线,同理有∠ADE=∠BDN=20°,∠ODH=20°,得结论.
(1)证明:如图1,
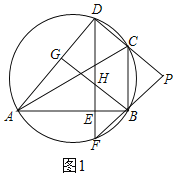
∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(2)由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,∵AB=![]() DH,
DH,
∴tan∠ACB=![]() ,
,
∴∠ACB=60°,∠BAC=30°,
∴∠ADB=60°,BC=![]() AC,
AC,
∴DH=![]() AC,
AC,
①当点O在DE的左侧时,如图2,作直径DM,连接AM、OH,则∠DAM=90°,
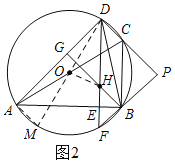
∴∠AMD+∠ADM=90°
∵DE⊥AB,
∴∠BED=90°,
∴∠BDE+∠ABD=90°,
∵∠AMD=∠ABD,
∴∠ADM=∠BDE,
∵DH=![]() AC,
AC,
∴DH=OD,
∴∠DOH=∠OHD=80°,
∴∠ODH=20°
∵∠AOB=60°,
∴∠ADM+∠BDE=40°,
∴∠BDE=∠ADM=20°,
②当点O在DE的右侧时,如图3,作直径DN,连接BN,
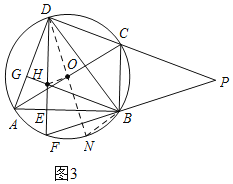
由①得:∠ADE=∠BDN=20°,∠ODH=20°,
∴∠BDE=∠BDN+∠ODH=40°,
综上所述,∠BDE的度数为20°或40°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. ![]() 一定是一次函数
一定是一次函数
B. 有的实数在数轴上找不到对应的点
C. 长为![]() 的三条线段能组成直角三角形
的三条线段能组成直角三角形
D. 无论![]() 为何值,点
为何值,点![]() 总是在第二象限
总是在第二象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为![]() 、宽为
、宽为![]() 的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为
的长方形白纸,按如图所示的方法黏合起来,黏合部分宽为![]() .
.

(1)根据上图,将表格补充完整:
白纸张数 | 1 | 2 | 3 | 4 | … | 10 | … |
纸条长度 | 40 | 75 | 110 | … | … |
(2)设![]() 张白纸黏合后的总长度为
张白纸黏合后的总长度为![]() ,则
,则![]() 与
与![]() 之间的关系式是 ;
之间的关系式是 ;
(3)你认为白纸黏合起来总长度可能为![]() 吗?为什么?
吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
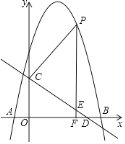
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 在
在![]() 轴上方的抛物线上,当
轴上方的抛物线上,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 若点
若点![]() ’是点
’是点![]() 关于直线
关于直线![]() 的对称点,当点
的对称点,当点![]() ’落在
’落在![]() 轴上时,请直接写出
轴上时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
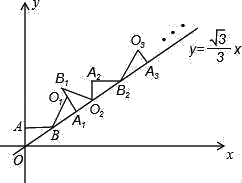
【题目】如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y=![]() x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=![]() x上,依次进行下去…,若点A的坐标是(0,1),则点A8的横坐标是_____
x上,依次进行下去…,若点A的坐标是(0,1),则点A8的横坐标是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com