
如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)①写出图1中的一对全等三角形;②写出图1中线段DE、AD、BE所具有的等量关系;(不必说明理由)
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE的理由;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由)。
(1)①△ADC≌△CEB,②DE=CE+CD=AD+BE。 (2)证明△ADC≌△CEB,得CE=AD,CD=BE。
所以DE=CE-CD=AD-BE (3)DE=BE
解析试题分析:解:(1)①如图1,在△ABC中,∠ACB=90°, ,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,
,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E, ,
, ,
, ;因为
;因为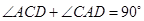 ,所以
,所以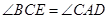 ,又因为AC=BC,所以△ADC≌△CEB,
,又因为AC=BC,所以△ADC≌△CEB,
②由①的结论知△ADC≌△CEB,所以CD=BE,AD=CE,所以
DE=CE+CD=AD+BE。
(2)∵AD⊥MN于D,BE⊥MN于E。
∴∠ADC=∠BEC=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°。
∴∠CAD=∠BCE。
在△ADC和△CEB中 ,
,
∴△ADC≌△CEB。
∴CE=AD,CD=BE。
∴DE=CE-CD=AD-BE。
(3)当MN旋转到图3的位置时,AD、DE、根据旋转的特征,结合(1)、(2)DE、AD、BE所满足的等量关系是DE=BE (或AD=
(或AD= ,BE=AD+DE等)。
,BE=AD+DE等)。
考点:全等三角形,旋转
点评:本题考查全等三角形,解答本题的关键是掌握全等三角形的判定方法,会证明两个三角形全等,熟悉旋转的特征,会利用旋转的特征来解答本题


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
| PE |
| CE |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 明理由.
明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| BC2+CD2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
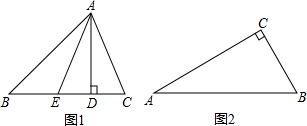 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=| DE |
| BD |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com