练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

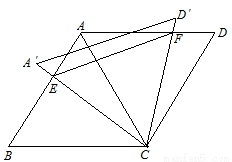
    如图,菱形ABCD中,边长为2,∠B=60°,将△ACD绕点C旋转，当AC（即A′C）与AB交于一点E,CD（即CD′）同时与AD交于一点F时,点E，F和点A构成△AEF。试探究△AEF的周长是否存在最小值,如果不存在，请说明理由；如果存在,请计算出△AEF周长的最小值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：云南昆明市 2017年九年级数学中考模拟试卷（含答案） 题型：单选题

    丽华根据演讲比赛中九位评委所给的分数作了如下表格：

    如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（ ）

    A. 平均数 B. 众数 C. 方差 D. 中位数

    查看答案和解析>>

    科目：初中数学 来源：重庆合川区清平中学 2017年九年级数学中考模拟试卷（含答案） 题型：解答题

    解方程：2x2﹣3x﹣1=0．

    查看答案和解析>>

    科目：初中数学 来源：重庆合川区清平中学 2017年九年级数学中考模拟试卷（含答案） 题型：单选题

    若方程(m-1)xm2+1-(m+1)x-2=0是一元二次方程,则m的值为 ( )

    A. 0 B. ±1 C. 1 D. -1

    查看答案和解析>>

    科目：初中数学 来源：九年级数学（浙教版）上册同步练习：1.4 二次函数的应用(三) 题型：解答题

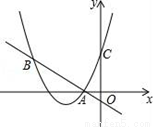
    如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．

    （1）求二次函数与一次函数的解析式；

    （2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：广西南宁市 2017年九年级数学中考模拟试卷（含答案） 题型：解答题

    如图，在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C，灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行，上午10：00在A处测得灯塔C位于轮船的北偏西30°方向，上午10：40在B处测得灯塔C位于轮船的北偏东60°方向，且与灯塔C相距12km.

    (1)若轮船照此速度与航向航向，何时到达海岸线？

    (2)若轮船不改变航向，该轮船能否停靠在码头？请说明理由(参考数据： ≈1.4， ≈1.7)．

    查看答案和解析>>

    科目：初中数学 来源：广西南宁市 2017年九年级数学中考模拟试卷（含答案） 题型：填空题

    计算：(﹣2)﹣1﹣|﹣3|=________．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2016-2017学年八年级5月单元测试数学试卷 题型：解答题

    如图，E、F分别是□ABCD的边BC、AD上的点，且BE＝DF．

    (1)求证：四边形AECF是平行四边形；

    (2)若BC＝10，∠BAC＝90°，且四边形AECF是菱形，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源：安徽省合肥市中铁国际城校区2016-2017学年八年级下学期第一次月考数学试卷 题型：单选题

    下列各式中是二次根式的是（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案