
【题目】甲、乙两家园林公司承接了哈尔滨市平房区园林绿化工程,已知乙公司单独完成所需要的天数是甲公司单独完成所需天数的1.5倍,如果甲公司单独工作10天,再由乙公司单独工作15天,这样就可完成整个工程的三分之二.
(1)求甲、乙两公司单独完成这项工程各需多少天?
(2)上级要求该工程完成的时间不得超过30天.甲、乙两公司合作若干天后,甲公司另有项目离开,剩下的工程由乙公司单独完成,并且在规定时间内完成,求甲、乙两公司合作至少多少天?
【答案】
(1)解:设甲公司单独x天完成,则乙公司单独完成此工程的天数为1.5x,由题意得
![]() +
+ ![]() =
= ![]() ,
,
解得:x=30.
经检验,x=30是原方程的解.
则1.5x=45.
答:甲、乙两公司单独完成这项工程各需30天、45天
(2)解:设甲、乙两公司合作a天可完成整个工程,由题意得
![]() a+
a+ ![]() ≥1,
≥1,
解得a≥10.
答:甲、乙两公司合作至少10天
【解析】(1)题中有两个等量关系,“乙公司单独完成所需要的天数是甲公司单独完成所需天数的1.5倍”,这是说明甲乙两队工作天数的关系,因此若设甲公司单独x天完成,则乙公司单独完成此工程的天数为1.5x;另一个等量关系:甲公司单独工作10天,再由乙公司单独工作15天,这样就可完成整个工程的三分之二.可得:甲公司单独工作10天完成的工作量+乙公司单独工作15天完成的工作量= ![]() ;(2)设甲、乙两公司合作a天可完成整个工程,等量关系为:甲公司工作a天完成的工作量+乙公司工作30天完成的工作量≥1,依此列出不等式求解即可.
;(2)设甲、乙两公司合作a天可完成整个工程,等量关系为:甲公司工作a天完成的工作量+乙公司工作30天完成的工作量≥1,依此列出不等式求解即可.
【考点精析】掌握分式方程的应用是解答本题的根本,需要知道列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点.
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于D点.
①当△ABC的面积为1时,求a的值.
②当△ABC的面积与△ABD的面积相等时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;
②3b+c+6=0;
③当x2+bx+c> ![]() 时,x>2;
时,x>2;
④当1<x<3时,x2+(b﹣1)x+c<0,
其中正确的序号是( )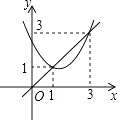
A.①②④
B.②③④
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止). 
(1)请你用画树状图或列表格的方法,求点(x,y)落在第二象限内的概率;
(2)直接写出点(x,y)落在函数y=﹣ ![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在等腰Rt△ABC中,∠C=90°,斜边AB=2,若将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F(点E不与A点重合,点F不与B点重合),且点C落在AB边上,记作点D.过点D作DK⊥AB,交射线AC于点K,设AD=x,y=cot∠CFE, 
(1)求证:△DEK∽△DFB;
(2)求y关于x的函数解析式并写出定义域;
(3)联结CD,当 ![]() =
= ![]() 时,求x的值.
时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com