
 ,问小鸟妈妈从D处飞到B处至少要飞行多少米?(D、C、B三点共线)
,问小鸟妈妈从D处飞到B处至少要飞行多少米?(D、C、B三点共线)
 ,小树高为4米,即CE=4米,就可以求出ED的长,根据CE∥AB,得到
,小树高为4米,即CE=4米,就可以求出ED的长,根据CE∥AB,得到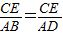 就可以求出AB,在直角△ABD中,根据勾股定理就可以得到BD的长.
就可以求出AB,在直角△ABD中,根据勾股定理就可以得到BD的长. ,
,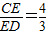 ,
,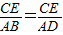 ,
,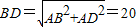 米.
米. ,CE=4,
,CE=4,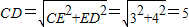 ,
,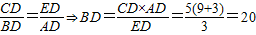 米.
米.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《四边形》(06)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 x2+bx+c过点A和点B,与y轴交于C点.
x2+bx+c过点A和点B,与y轴交于C点. )(m<0)在抛物线y=
)(m<0)在抛物线y= x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值;
x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值;
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《平面直角坐标系》(02)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年四川省内江市二中中考数学一模试卷(解析版) 题型:解答题
 x2+bx+c过点A和点B,与y轴交于C点.
x2+bx+c过点A和点B,与y轴交于C点. )(m<0)在抛物线y=
)(m<0)在抛物线y= x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值;
x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值;
查看答案和解析>>
科目:初中数学 来源:2008年湖南省岳阳市中考数学试卷(解析版) 题型:解答题
 x2+bx+c过点A和点B,与y轴交于C点.
x2+bx+c过点A和点B,与y轴交于C点. )(m<0)在抛物线y=
)(m<0)在抛物线y= x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值;
x2+bx+c的图象上,点P为此抛物线对称轴上的一个动点,求PQ+PB的最小值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com