
分析 (1)把点A(-5,0),B(-1,0)代入二次函数y=-12x2+bx+c,求出b、c的值即可得出结论;
(2)把(1)中二次函数的解析式化为顶点式的形式,再根据二次函数图象平移的方法即可得出结论.
解答 解:(1)∵二次函数y=-12x2+bx+c的图象与x轴相交于A(-5,0),B(-1,0),
∴$\left\{\begin{array}{l}-12×25-5b+c=0\\-12-b+c=0\end{array}\right.$,解得$\left\{\begin{array}{l}b=-72\\ c=-60\end{array}\right.$,
∴这个二次函数的关系式为:y=-12x2-72x-60;
(2)∵二次函数的关系式为y=-12x2-72x-60=-12(x+3)2+48,
∴函数的顶点坐标为(-3,48),
∴这个函数的图象与x轴只有一个交点时应将函数图象先向下平移48个单位,再向右平移3个单位.
点评 本题考查的是抛物线与x轴的交点及二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解答此题的关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
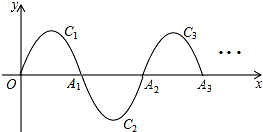 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O和A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,…如此进行下去,得到一条“波浪线”.若点P(41,m)在此“波浪线”上,则m的值为( )| A. | 2 | B. | -2 | C. | 0 | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
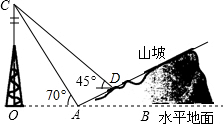 如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)
如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.
如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )| A. | (6$\sqrt{3}$-$\frac{4}{3}$π)m2 | B. | (8$\sqrt{3}$-$\frac{4}{3}$π)m2 | C. | (6$\sqrt{3}$-$\frac{8}{3}$π)m2 | D. | (8$\sqrt{3}$-$\frac{8}{3}$π)m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com