
【题目】如图,在△ABC中,∠B与∠C的角平分线相交于点I,过点I作BC的平行线,分别交AB、AC于点D、E.若AB=9,AC=6,BC=8,则△ADE的周长是( )
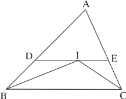
A. 14B. 15C. 17D. 23
【答案】B
【解析】
根据角平分线的定义得∠DBI=∠CBI,∠ECI=∠BCI,再根据平行线的性质得∠DFB=∠CBI,∠BCI=∠EIC,则∠DBI=∠DIB,∠ECI=∠EIC,根据平行线的判定得DB=DI,EI=EC,再根据三角形的定义得△ADE的周长= AD+DE+AE=AD+DI+AE+EI=AD+DB+AE+CE=AB+AC
∵BI、CI分别平分∠ABC和∠ACB,
∴∠ABI=∠CBI,∠ACI=∠BCI.
∵DE∥BC,
∴∠DIB=∠IBC,∠BCI=∠EIC.
∴∠ABI=∠DIB,∠EIC=∠ACI.
∴DB=DI,EI=EC.
∴L△ADE=AD+DE+AE=AD+DI+AE+EI=AD+DB+AE+CE=AB+AC=9+6=15.
故选:B.


科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,由于该十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .
.
(1)假设平均每天通过该路口的汽车为5 000辆,求汽车在此向左转、向右转、直行的车辆各是多少辆;
(2)目前在此路口,汽车向左转、向右转、直行的绿灯亮的时间都为30 s,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你利用概率的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )
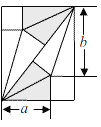
A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
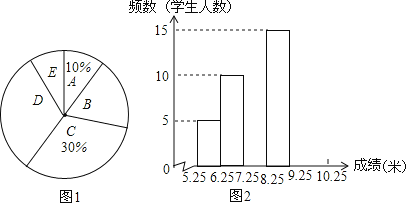
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 的平分线
的平分线![]() 与外角
与外角![]() 的平分线
的平分线![]() 所在的直线交于点
所在的直线交于点![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在
落在![]() 处.
处.
①当![]() 时,求
时,求![]() 的度数;②试确定
的度数;②试确定![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
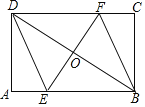
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
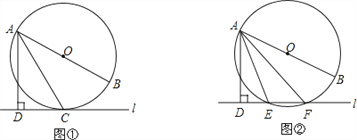
【题目】已知直线![]() 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥![]() 于点D.
于点D.
(1)如图①,当直线![]() 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线![]() 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与证明:
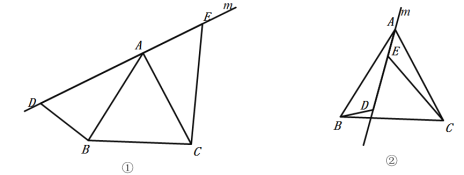
(1)如图①,直线![]() 经过正三角形
经过正三角形![]() 的顶点
的顶点![]() ,在直线
,在直线![]() 上取点
上取点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明;
之间满足的数量关系,并予以证明;
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图②的位置,
逆时针方向旋转一个角度到如图②的位置,![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com