
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжа![]() жБЯп
жБЯп![]() гыxжсЁЂyжсЯрНЛгкAЁЂBСНЕуЃЌЖЏЕуCдкЯпЖЮOAЩЯЃЌНЋЯпЖЮCBШЦзХЕуCЫГЪБеыа§зЊ
гыxжсЁЂyжсЯрНЛгкAЁЂBСНЕуЃЌЖЏЕуCдкЯпЖЮOAЩЯЃЌНЋЯпЖЮCBШЦзХЕуCЫГЪБеыа§зЊ![]() ЕУЕНCDЃЌДЫЪБЕуDЧЁКУТфдкжБЯпABЩЯЪБЃЌЙ§ЕуDзї
ЕУЕНCDЃЌДЫЪБЕуDЧЁКУТфдкжБЯпABЩЯЪБЃЌЙ§ЕуDзї![]() жсгкЕуEЃЎ
жсгкЕуEЃЎ
![]() ЧѓжЄЃК
ЧѓжЄЃК![]() Ёе
Ёе![]() ЃЛ
ЃЛ
![]() ШчЭМ2ЃЌНЋ
ШчЭМ2ЃЌНЋ![]() биxжсе§ЗНЯђЦНвЦЕУ
биxжсе§ЗНЯђЦНвЦЕУ![]() ЃЌЕБжБЯп
ЃЌЕБжБЯп![]() ОЙ§ЕуDЪБЃЌЧѓЕуDЕФзјБъМА
ОЙ§ЕуDЪБЃЌЧѓЕуDЕФзјБъМА![]() ЦНвЦЕФОрРыЃЛ
ЦНвЦЕФОрРыЃЛ
![]() ШєЕуPдкyжсЩЯЃЌЕуQдкжБЯпABЩЯ
ШєЕуPдкyжсЩЯЃЌЕуQдкжБЯпABЩЯ![]() ЪЧЗёДцдквдCЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФQЕузјЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЪЧЗёДцдквдCЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФQЕузјЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]() ЦНвЦЕФОрРыЪЧ
ЦНвЦЕФОрРыЪЧ![]() ИіЕЅЮЛЃЎЃЈ3ЃЉЕуQЕФзјБъЮЊ
ИіЕЅЮЛЃЎЃЈ3ЃЉЕуQЕФзјБъЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
![]() ИљОнAASЛђASAМДПЩжЄУїЃЛ
ИљОнAASЛђASAМДПЩжЄУїЃЛ
![]() ЪзЯШЧѓГіЕуDЕФзјБъЃЌдйЧѓГіжБЯп
ЪзЯШЧѓГіЕуDЕФзјБъЃЌдйЧѓГіжБЯп![]() ЕФНтЮіЪНЃЌЧѓГіЕу
ЕФНтЮіЪНЃЌЧѓГіЕу![]() ЕФзјБъМДПЩНтОіЮЪЬтЃЛ
ЕФзјБъМДПЩНтОіЮЪЬтЃЛ
![]() ШчЭМ3жаЃЌзї
ШчЭМ3жаЃЌзї![]() НЛyжсгкPЃЌзї
НЛyжсгкPЃЌзї![]() НЛABгкQЃЌдђЫФБпаЮPCDQЪЧЦНааЫФБпаЮЃЌЧѓГіжБЯпPCЕФНтЮіЪНЃЌПЩЕУЕуPзјБъЃЌЕуCЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ
НЛABгкQЃЌдђЫФБпаЮPCDQЪЧЦНааЫФБпаЮЃЌЧѓГіжБЯпPCЕФНтЮіЪНЃЌПЩЕУЕуPзјБъЃЌЕуCЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕУЕНPЃЌЭЦГіЕуDЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ
ИіЕЅЮЛЕУЕНPЃЌЭЦГіЕуDЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕУЕНQЃЌдйИљОнЖдГЦадПЩЕУ
ИіЕЅЮЛЕУЕНQЃЌдйИљОнЖдГЦадПЩЕУ![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
![]() жЄУїЃК
жЄУїЃК![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() Ёе
Ёе![]() ЃЎ
ЃЎ
![]() Ёе
Ёе![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Аб![]() ДњШы
ДњШы![]() ЕУЕНЃЌ
ЕУЕНЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() жБЯпBCЕФНтЮіЪНЮЊ
жБЯпBCЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЩшжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌАб
ЃЌАб![]() ДњШыЕУЕН
ДњШыЕУЕН![]() ЃЌ
ЃЌ
![]() жБЯп
жБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЦНвЦЕФОрРыЪЧ
ЦНвЦЕФОрРыЪЧ![]() ИіЕЅЮЛЃЎ
ИіЕЅЮЛЃЎ
![]() НтЃКШчЭМ3жаЃЌзї
НтЃКШчЭМ3жаЃЌзї![]() НЛyжсгкPЃЌзї
НЛyжсгкPЃЌзї![]() НЛABгкQЃЌдђЫФБпаЮPCDQЪЧЦНааЫФБпаЮЃЌ
НЛABгкQЃЌдђЫФБпаЮPCDQЪЧЦНааЫФБпаЮЃЌ
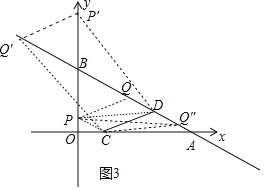
взжЊжБЯпPCЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕуCЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ
ЕуCЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕУЕНPЃЌ
ИіЕЅЮЛЕУЕНPЃЌ
![]() ЕуDЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ
ЕуDЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЯђЩЯЦНвЦ![]() ИіЕЅЮЛЕУЕНQЃЌ
ИіЕЅЮЛЕУЕНQЃЌ
![]() ЃЌ
ЃЌ
ЕБCDЮЊЖдНЧЯпЪБЃЌЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌПЩЕУ
ЪЧЦНааЫФБпаЮЃЌПЩЕУ![]() ЃЌ
ЃЌ
ЕБЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЪБЃЌПЩЕУ
ЮЊЦНааЫФБпаЮЪБЃЌПЩЕУ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуQЕФзјБъЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬНЫїЙцТЩЃКЙлВьЯТУцгЩзщГЩЕФЭМАИКЭЫуЪНЃЌНтД№ЮЪЬтЃК
1+3ЃН4ЃН22
1+3+5ЃН9ЃН32
1+3+5+7ЃН16ЃН42
1+3+5+7+9ЃН25ЃН52
ЃЈ1ЃЉЧыМЦЫу 1+3+5+7+9+11ЃЛ
ЃЈ2ЃЉЧыМЦЫу 1+3+5+7+9+Ё+19ЃЛ
ЃЈ3ЃЉЧыМЦЫу 1+3+5+7+9+Ё+ЃЈ2nЉ1ЃЉЃЛ
ЃЈ4ЃЉЧыгУЩЯЪіЙцТЩМЦЫуЃК21+23+25+Ё+99ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕу C ЪЧЯпЖЮ AB ЩЯвЛЕуЃЌЧв 5BC=2ABЃЌD ЪЧ AB ЕФжаЕуЃЌE ЪЧCB ЕФжаЕуЃЌЃЈ1ЃЉШє DE=6ЃЌЧѓ AB ЕФГЄЃЛЃЈ2ЃЉЧѓ ADЃКAC.
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЦНЗжЁЯBACЃЌЧвBD=CDЃЌDEЁЭABгкЕуEЃЌDFЁЭACгкЕуFЃЎ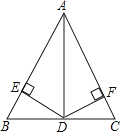
ЃЈ1ЃЉЧѓжЄЃКAB=ACЃЛ
ЃЈ2ЃЉШєAD=2 ![]() ЃЌЁЯDAC=30ЁуЃЌЧѓACЕФГЄЃЎ
ЃЌЁЯDAC=30ЁуЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABОЙ§ЁбOЩЯЕФЕуCЃЌжБЯпAOгыЁбOНЛгкЕуEКЭЕуDЃЌOBгыЁбOНЛгкЕуFЃЌСЌНгDFЁЂDCЃЎвбжЊOA=OBЃЌCA=CBЃЌDE=10ЃЌDF=6ЃЎ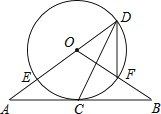
ЃЈ1ЃЉЧѓжЄЃКЂйжБЯпABЪЧЁбOЕФЧаЯпЃЛЂкЁЯFDC=ЁЯEDCЃЛ
ЃЈ2ЃЉЧѓCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌжБЯпy=Љ ![]() x+3гыxжсЁЂyжсЗжБ№НЛгкЕуBКЭЕуCЃЌСЌНгACЃЌЖЅЕуЮЊDЕФХзЮяЯпy=ax2+bx+cЙ§AЁЂBЁЂCШ§ЕуЃЎ
x+3гыxжсЁЂyжсЗжБ№НЛгкЕуBКЭЕуCЃЌСЌНгACЃЌЖЅЕуЮЊDЕФХзЮяЯпy=ax2+bx+cЙ§AЁЂBЁЂCШ§ЕуЃЎ 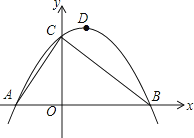
ЃЈ1ЃЉЧыжБНгаДГіBЁЂCСНЕуЕФзјБъЃЌХзЮяЯпЕФНтЮіЪНМАЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉЩшХзЮяЯпЕФЖдГЦжсDEНЛЯпЖЮBCгкЕуEЃЌPЪЧЕквЛЯѓЯоФкХзЮяЯпЩЯвЛЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛЯпЖЮBCгкЕуFЃЌШєЫФБпаЮDEFPЮЊЦНааЫФБпаЮЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕуMЪЧЯпЖЮBCЩЯЕФвЛЖЏЕуЃЌЙ§ЕуMзїMNЁЮABЃЌНЛACгкЕуNЃЌЕуQДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮBAЯђЕуAдЫЖЏЃЌдЫЖЏЪБМфЮЊtЃЈУыЃЉЃЌЕБtЃЈУыЃЉЮЊКЮжЕЪБЃЌДцдкЁїQMNЮЊЕШбќжБНЧШ§НЧаЮЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗНИёжагавЛЬѕУРРіПЩАЎЕФаЁН№гуЃЎ

(1)ШєЗНИёЕФБпГЄЮЊ1ЃЌдђаЁгуЕФУцЛ§ЮЊ ЃЎ
(2)ЛГіаЁгуЯђзѓЦНвЦ3ИёКѓЕФЭМаЮЃЈВЛвЊЧѓаДзїЭМВНжшКЭЙ§ГЬЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛМўЙЄГЬМзЖРзі50ЬьПЩЭъЃЌввЖРзі75ЬьПЩЭъЃЌЯждкСНИіШЫКЯзїЃЌЕЋЪЧжаЭОвввђЪТРыПЊМИЬьЃЌДгПЊЙЄКѓ40ЬьАбетМўЙЄГЬзіЭъЃЌдђввжаЭОРыПЊСЫЃЈЁЁЁЁЃЉЬьЃЎ
A. 10 B. 20 C. 30 D. 25
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌAB=ACЃЌАбЁїABCШЦAЕубиЫГЪБеыЗНЯђа§зЊЕУЕНЁїADEЃЌСЌНгBDЃЌCEНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAECЁеЁїADBЃЛ
ЃЈ2ЃЉШєAB=2ЃЌЁЯBAC=45ЁуЃЌЕБЫФБпаЮADFCЪЧСтаЮЪБЃЌЧѓBFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com