
【题目】在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:
①AB=![]() ; ②当点E与点B重合时,MH=
; ②当点E与点B重合时,MH=![]() ; ③AF+BE=EF;④F、E分别不与端点A、B重合时,总有S△AGF+ S△EBH= S△FEM,其中正确结论为--------------------------( )
; ③AF+BE=EF;④F、E分别不与端点A、B重合时,总有S△AGF+ S△EBH= S△FEM,其中正确结论为--------------------------( )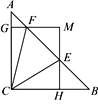
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】B
【解析】(1)∵在△ABC中,∠ACB=90,AC=BC=1,
∴AB=![]() ,故①正确;
,故①正确;
(2)如下图1,当点E与点B重合时,点H与点B重合,
∴MB⊥BC,∠MBC=90°,
∵MG⊥AC,
∴∠MGC=∠C=∠MBC=90°,
∴MG∥BC,四边形MGCB是矩形,
∴MH=MB=CG,
∵∠FCE=45°=∠ABC,∠A=45°=∠ACF,
∴AF=CF=BF,
∴FG是△ACB的中位线,
∴GC=![]() AC=
AC=![]() ,
,
∴MH=GC=![]() ,故②正确;
,故②正确;
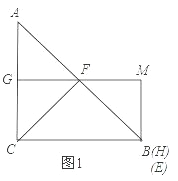
(3)如下图2所示,
∵AC=BC,∠ACB=90°,
∴∠A=∠5=45°.
将△ACF顺时针旋转90°至△BCD,则CF=CD,∠1=∠4,∠A=∠6=45°,BD=AF;
∵∠2=45°,
∴∠1+∠3=∠3+∠4=45°,
∴∠DCE=∠2,
∵在△ECF和△ECD中,CF=CD,∠2=∠DCE,CE=CE,
∴△ECF≌△ECD(SAS),
∴EF=DE,
∵∠5=45°,
∴∠BDE=90°,
∴DE2=BD2+BE2,即EF2=AF2+BE2,故③错误;
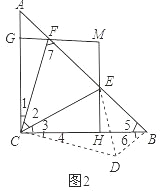
(4)∵△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵MG⊥AC,MH⊥BC,
∴∠AGF=∠BHE=90°,
∴∠AFG=∠BEH=45°,
∴∠MFE=∠AFG=45°,∠MEF=∠BEH=45°,
∴△AGF、△BEH、△MEF都是等腰直角三角形,
∴AG=FG=![]() AF,BH=HE=
AF,BH=HE=![]() BE,ME=MF=
BE,ME=MF=![]() EF,
EF,
∴S△AGF=![]() AF2,S△BEH=
AF2,S△BEH=![]() BE2,S△MEF=
BE2,S△MEF=![]() EF2,
EF2,
∵EF2=AF2+BE2,
∴S△AGF+S△BEH=S△MEF,故④正确.
综上所述,正确的结论是①②④.
故选B.


科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点 F,∠ADB=30°,则EF=---------------------------------------------( )

A. 3![]() B. 2
B. 2![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
(1)如果∠AOC=50°,求∠MON的度数;
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.
(1)求m的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向左移动![]() 到达
到达![]() 点,再向左移动
点,再向左移动![]() 到达
到达![]() 点,然后向右移动
点,然后向右移动![]() 到达
到达![]() 点
点
(1)用1个单位长度表示![]() ,请你在数轴上表示出
,请你在数轴上表示出![]() 、
、![]() 、
、![]() 三点的位置;
三点的位置;
![]()
(2)把点![]() 到点
到点![]() 的距离记为
的距离记为![]() ,则
,则![]() =_______
=_______ ![]() .
.
(3)若点![]() 以每秒
以每秒![]() 的速度向左移动,同时
的速度向左移动,同时![]() 、
、![]() 点分别以每秒
点分别以每秒![]() 、
、![]() 的速度向右移动.设移动时间为
的速度向右移动.设移动时间为![]() 秒,试探索:
秒,试探索: ![]() 的值是否会随着
的值是否会随着![]() 的变化而改变?请说明理由.
的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2 , y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com