
【题目】菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.
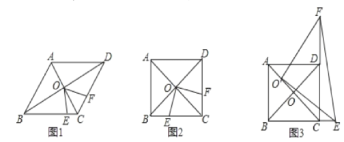
(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系___;
(2)如图1,当∠ABC=90°时,若AC=4![]() ,BE=
,BE=![]() ,求线段EF的长;
,求线段EF的长;
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
【答案】(1)CE+CF=![]() AB;(2)
AB;(2)![]() ;(3)CFCE =
;(3)CFCE =![]() O`C.
O`C.
【解析】
(1)如图1中,连接EF,在CO上截取CN=CF,只要证明△OFN≌△EFC,即可推出CE+CF=OC,再证明OC=![]() AB即可.
AB即可.
(2)先证明△OBE≌△OCF得到BE=CF,在Rt△CEF中,根据CE![]() +CF
+CF![]() =EF
=EF![]() 即可解决问题.
即可解决问题.
(3)结论:CF-CE=![]() O`C,过点O`作O`H⊥AC交CF于H,只要证明△FO`H≌△EO
O`C,过点O`作O`H⊥AC交CF于H,只要证明△FO`H≌△EO![]() C,推出FH=CE,再根据等腰直角三角形性质即可解决问题.
C,推出FH=CE,再根据等腰直角三角形性质即可解决问题.
(1)结论CE+CF=![]() AB.
AB.
理由:如图1中,连接EF,在CO上截取CN=CF.

∵∠EOF+∠ECF=180°,
∴O、E. C. F四点共圆,
∵∠ABC=60°,四边形ABCD是菱形,
∴∠BCD=180°∠ABC=120°,
∴∠ACB=∠ACD=60°,
∴∠OEF=∠OCF,∠OFE=∠OCE,
∴∠OEF=∠OFE=60°,
∴△OEF是等边三角形,
∴OF=FE,
∵CN=CF,∠FCN=60°,
∴△CFN是等边三角形,
∴FN=FC,∠OFE=∠CFN,
∴∠OFN=∠EFC,
在△OFN和△EFC中,
 ,
,
∴△OFN≌△EFC,
∴ON=EC,
∴CE+CF=CN+ON=OC,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠CBO=30°,AC⊥BD,
在RT△BOC中,∵∠BOC=90°,∠OBC=30°,
∴OC=![]() BC=
BC=![]() AB,
AB,
∴CE+CF=![]() AB.
AB.
(2)连接EF

∵在菱形ABCD中
∴菱形ABCD是正方形,
∴∠BOC=90°,OB=OC,AB=AC,∠OBE=∠OCF=45°,∠BCD=90°
∵∠EOF+∠BCD=180°,
∴∠EOF=90°,
∴∠BOE=∠COF
∴△OBE≌△OCF,
∴BE=CF,
∵BE=![]() ,
,
∴CF=![]() ,
,
在Rt△ABC中,AB![]() +BC
+BC![]() =AC
=AC![]() ,AC=4
,AC=4![]()
∴BC=4,
∴CE=![]() ,
,
在Rt△CEF中,CE![]() +CF
+CF![]() =EF
=EF![]() ,
,
∴EF=![]()
答:线段EF的长为![]() ,
,
(3)结论:CFCE=![]() O`C.
O`C.
理由:过点O`作O`H⊥AC交CF于H,

∵∠O`CH=∠O`HC=45°,
∴O`H=O`C,
∵∠FO`E=∠HO`C,
∴∠FO`H=∠CO`E,
∵∠EO`F=∠ECF=90°,
∴O`.C. F. E四点共圆,
∴∠O`EF=∠OCF=45°,
∴∠O`FE=∠O`EF=45°,
∴O`E=O`F,
在△FO`H和△EO`C中,
 ,
,
∴△FO`H≌△EO![]() C,
C,
∴FH=CE,
∴CFCE=CFFH=CH=![]() O`C.
O`C.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造ΔABD的轴对称图形ΔABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.
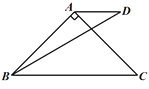
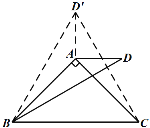
图1 图2
(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决老师布置的这道作业题.
查看答案和解析>>
科目:初中数学 来源: 题型:
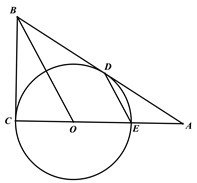
【题目】如图,在![]() ,O是AC上的一点,
,O是AC上的一点, ![]() 与BC,AB分别切于点C,D, 与AC相交于点E,连接BO.
与BC,AB分别切于点C,D, 与AC相交于点E,连接BO.
(1) 求证:CE2=2DE![]() BO;
BO;
(2) 若BC=CE=6,则AE= ,AD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
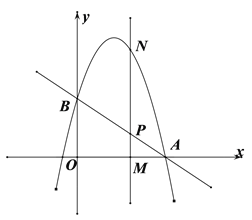
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 当
当![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两校举行初中数学联赛,各校从九年级学生中挑选50人参加,成绩统计如下表:
成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | A | 2 | 5 | 10 | 13 | 14 | 6 |
B | 4 | 4 | 16 | 2 | 12 | 12 | |
请你根据所学知识和表中数据,判断这两校学生在这次联赛中的成绩谁优谁次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节约用水,某区规定三口之家每月标准用水量为15立方米,不超过标准的水费价格为每立方米1.5元,超过标准的超过部分的价格为每立方米3元,小明家11月份用水x立方米;小红家11月份用水y(y>15)立方米
(1)用含y的代数式表示小红家11月份应缴的水费;
(2)用含有x的代数式表示小明家11月份应缴的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点![]() 、
、![]() 在数轴上分别表示实数
在数轴上分别表示实数![]() ,
,![]() ,
,![]() 、
、![]() 两点之间的距高表示为
两点之间的距高表示为![]()
当![]() 、
、![]() 两点中有一点在原点时,不妨设点
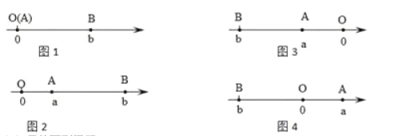
两点中有一点在原点时,不妨设点![]() 在原点,如图1,
在原点,如图1,![]() ;
;
当![]() 、
、![]() 都不在原点时,
都不在原点时,
①如图2,点![]() 、
、![]() 都在原点的右侧,
都在原点的右侧,![]() ;
;
②如图3,点![]() 、
、![]() 都在原点的左侧,
都在原点的左侧,![]() ;
;
③如图4,点![]() 、
、![]() 在原点的两侧,
在原点的两侧,![]() ;
;
(2)回答下列问题:
①数轴上表示2和5的两点间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ;
②数轴上表示![]() 和-1的两点
和-1的两点![]() 和
和![]() 之间的距离是 ,如果
之间的距离是 ,如果![]() ,那么
,那么![]() 为 ;
为 ;
③当代数式![]() 取最小值时,相应的
取最小值时,相应的![]() 的取值范围是 ;
的取值范围是 ;
④求![]() 的最小值,提示:
的最小值,提示:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com