
【题目】在同一平面内,若一个点到一条直线的距离不大于1,则 称这个点是该直线的“邻点”.在平面直角坐标系中,已知点![]()
![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() 轴,并将
轴,并将![]() 进行平移,平移后点
进行平移,平移后点![]() 分别对应点
分别对应点![]() .
.
(1)点![]() (填写是或不是)直线
(填写是或不是)直线![]() 的“邻点”,请说明理由;
的“邻点”,请说明理由;
(2)若点![]() 刚好落在直线
刚好落在直线![]() 上,点
上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 落在
落在![]() 轴上,且
轴上,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标,判断点
的坐标,判断点![]() 是否是直线
是否是直线![]() 的“邻点”,并说明理由.
的“邻点”,并说明理由.
【答案】(1)是,理由见详解;(2)B点坐标为:![]() 或
或![]() ,B点不是直线
,B点不是直线![]() 的邻点.
的邻点.
【解析】
(1)求出点A到直线![]() 的距离即可判断;
的距离即可判断;
(2)先找到平移规则,然后由点E落在x轴上,求出a的值,根据三角形的面积,求出b的值,然后求得B点坐标,即可得到答案.
解:(1)点A是直线![]() 的邻点;
的邻点;
理由:∵![]() 则直线
则直线![]() 为:
为:![]()
∵点![]() ,
,
∴点A到直线![]() 的距离为:
的距离为:![]() ,
,
∵![]() ,
,
∴点A是直线![]() 的邻点,
的邻点,
故答案为:是.
(2)由题意,点F为:![]() ,
,
∵![]() →
→![]() ,
,
∴横坐标加上![]() ,纵坐标加上1,
,纵坐标加上1,
∴D点为![]() ,E点为
,E点为![]() ,
,
∵点![]() 落在
落在![]() 轴上,
轴上,
∴![]() ,解得:
,解得:![]() ,
,
∴D点为![]() ,点F为
,点F为![]() ,
,
∵![]() 的面积为
的面积为![]() ,则有
,则有
MF=![]() ,三角形的高为:
,三角形的高为:![]() ,
,
∴![]() ,
,
解得: ![]() ,
,
当![]() 时,
时,![]() ,则B点坐标为:
,则B点坐标为:![]() ,
,
∴点B到直线![]() 的距离为:
的距离为:![]() ,
,
∴点B不是直线![]() 的邻点;
的邻点;
当![]() 时,
时,![]() ,则点B坐标为:
,则点B坐标为:![]() ,
,
∴点B到直线![]() 的距离为:
的距离为:![]() ,
,
∴点B不是直线![]() 的邻点.
的邻点.


科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
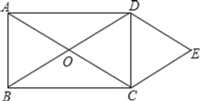
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE//AC,CE//BD,DE、CE相交于点E.
求证:(1)四边形OCED是菱形.
(2)连接OE,若AD=5,CD=3,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点为B(1,3),与
的顶点为B(1,3),与![]() 轴的交点A在点 (2,0)和(3,0)之间.以下结论:
轴的交点A在点 (2,0)和(3,0)之间.以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ≥
≥![]() ;⑤若
;⑤若![]() ,且
,且![]() ,
,
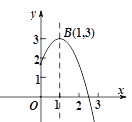
则![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:探究函数y=|x|-1的性质.
小凡同学根据学习函数的经验,对函数y=|x|-1的图象与性质进行了探究.下面是小凡的探究过程,请补充完整:
(1)在函数y=|x|-1中,自变量x的取值范围是______________;
(2)下表是y与x的几组对应值.
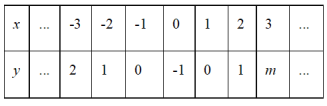
①m=_________;
②若A(n,9),B(10,9)为该函数图象上不同的两点,则n=__________;
(3)如下图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
(4)结合函数图象,解决问题:
①该函数有______(填“最大值”或“最小值”);并写出这个值为______;
②观察函数y=|x|-1的图象,写出该图象的两条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象法求方程的解,体现了数形结合的方法,它是将方程的解看成两个函数图象交点的横坐标.若关于x的方程x2+a﹣![]() =0(a>0)只有一个整数解,则a的值等于 .
=0(a>0)只有一个整数解,则a的值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A,B分别在x,y轴上,已知OA=3,点D为y轴上一点,其坐标为(0,1),CD=5,点P从点A出发以每秒1个单位的速度沿线段A﹣C﹣B的方向运动,当点P与点B重合时停止运动,运动时间为t秒
(1)求B,C两点坐标;
(2)①求△OPD的面积S关于t的函数关系式;
②当点D关于OP的对称点E落在x轴上时,求点E的坐标;
(3)在(2)②情况下,直线OP上求一点F,使FE+FA最小.
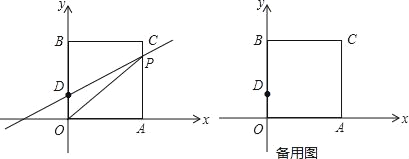
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com