
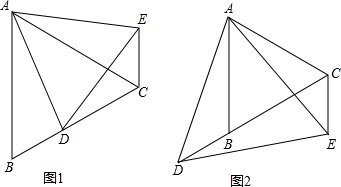
 等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连接CE.
等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连接CE. 证明:(1)如图1,∵△ADE与△ABC都是等边三角形,
证明:(1)如图1,∵△ADE与△ABC都是等边三角形,
|
|



科目:初中数学 来源: 题型:
 如图,已知等边△ABC,点O是BC上任意一点,OE、OF分别与两边垂直,等边三角形的高为1,则OE+OF的值为( )
如图,已知等边△ABC,点O是BC上任意一点,OE、OF分别与两边垂直,等边三角形的高为1,则OE+OF的值为( )| A、0.5 | B、1 | C、2 | D、不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市怀柔九年级上学期期末考试数学试卷(解析版) 题型:解答题
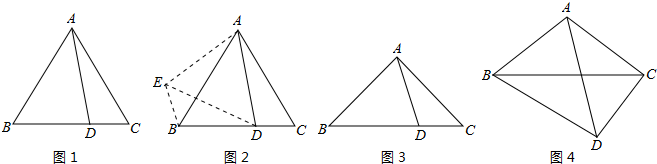
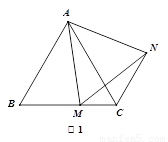
(1)如图1,在等边△ABC中,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等边△AMN,联结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是边BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.

【拓展延伸】
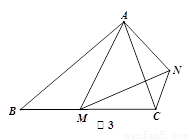
(3)如图3,在等腰△ABC中,BA=BC,点M是边BC上的任意一点(不含端点B、C),联结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.联结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 AD.
AD.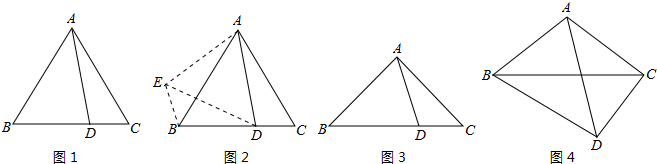
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com