
【题目】如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.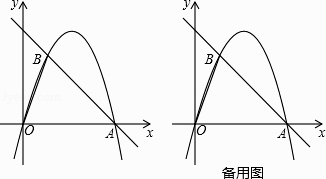
(1)求a,b的值;
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM//OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR//MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
【答案】
(1)
解:
∵y=﹣x+4与x轴交于点A,
∴A(4,0),
∵点B的横坐标为1,且直线y=﹣x+4经过点B,
∴B(1,3),
∵抛物线y=ax2+bx经过A(4,0),B(1,3),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴a=﹣1,b=4;
(2)
解:方法一:
如图,作BD⊥x轴于点D,延长MP交x轴于点E,
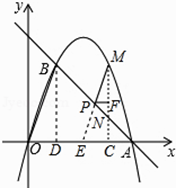
∵B(1,3),A(4,0),
∴OD=1,BD=3,OA=4,
∴AD=3,
∴AD=BD,
∵∠BDA=90°,∠BAD=∠ABD=45°,
∵MC⊥x轴,∴∠ANC=∠BAD=45°,
∴∠PNF=∠ANC=45°,
∵PF⊥MC,
∴∠FPN=∠PNF=45°,
∴NF=PF=t,
∵∠PFM=∠ECM=90°,
∴PF//EC,
∴∠MPF=∠MEC,
∵ME//OB,∴∠MEC=∠BOD,
∴∠MPF=∠BOD,
∴tan∠BOD=tan∠MPF,
∴ ![]() =
= ![]() =3,
=3,
∴MF=3PF=3t,
∵MN=MF+FN,
∴d=3t+t=4t;
方法二:
延长MP交x轴于点M′,作M′N′//MN交AB于N′,
延长FP交M′N′于F′,∵M′N′//MN,∴△PMN∽△PM′N′,
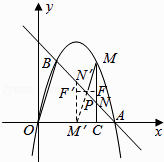
∴ ![]() ,∵O(0,0),B(1,3),
,∵O(0,0),B(1,3),
∴KOB=3,
∵PM//OB,
∴KPM=KOB=3,则lPM:y=3x+b,设P(p,﹣p+4),则b=4﹣4p,
∴lPM:y=3x+4﹣4P,把y=0代入,∴x= ![]() ,
,
∴M′( ![]() ,0),
,0),
∵N′x=M′x,把x= ![]() 代入y=﹣x+4,
代入y=﹣x+4,
∴y= ![]() ,
,
∴N′( ![]() ,
, ![]() ),∴M′N′=
),∴M′N′= ![]() ,
,
∵PF′⊥M′N′,
∴PF′=p﹣ ![]() =
= ![]() ,
,
∴ ![]() .
.
(3)
解:方法一:
如备用图,由(2)知,PF=t,MN=4t,
∴S△PMN= ![]() MN×PF=
MN×PF= ![]() ×4t×t=2t2,
×4t×t=2t2,
∵∠CAN=∠ANC,
∴CN=AC,
∴S△ACN= ![]() AC2,
AC2,
∵S△ACN=S△PMN,
∴ ![]() AC2=2t2,
AC2=2t2,
∴AC=2t,
∴CN=2t,
∴MC=MN+CN=6t,
∴OC=OA﹣AC=4﹣2t,
∴M(4﹣2t,6t),
由(1)知抛物线的解析式为:y=﹣x2+4x,
将M(4﹣2t,6t)代入y=﹣x2+4x得:
﹣(4﹣2t)2+4(4﹣2t)=6t,
解得:t1=0(舍),t2= ![]() ,
,
∴PF=NF= ![]() ,AC=CN=1,OC=3,MF=
,AC=CN=1,OC=3,MF= ![]() ,PN=
,PN= ![]() ,PM=
,PM= ![]() ,AN=
,AN= ![]() ,
,
∵AB=3 ![]() ,
,
∴BN=2 ![]() ,
,
作NH⊥RQ于点H,
∵QR//MN,
∴∠MNH=∠RHN=90°,∠RQN=∠QNM=45°,
∴∠MNH=∠NCO,
∴NH//OC,
∴∠HNR=∠NOC,
∴tan∠HNR=tan∠NOC,
∴ ![]() =
= ![]() =
= ![]() ,
,
设RH=n,则HN=3n,
∴RN= ![]() n,QN=3
n,QN=3 ![]() n,
n,
∴PQ=QN﹣PN=3 ![]() n﹣
n﹣ ![]() ,
,
∵ON= ![]() =
= ![]() ,
,
OB= ![]() =
= ![]() ,
,
∴OB=ON,∴∠OBN=∠BNO,
∵PM//OB,
∴∠OBN=∠MPB,
∴∠MPB=∠BNO,
∵∠MQR﹣∠BRN=45°,∠MQR=∠MQP+∠RQN=∠MQP+45°,
∴∠BRN=∠MQP,
∴△PMQ∽△NBR,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:n= ![]() ,
,
∴R的横坐标为:3﹣ ![]() =
= ![]() ,R的纵坐标为:1﹣
,R的纵坐标为:1﹣ ![]() =
= ![]() ,
,
∴R( ![]() ,
, ![]() ).
).
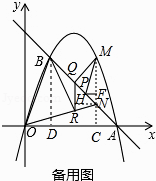
方法二:设M(t,﹣t2+4t),N(t,﹣t+4),
∴MN=﹣t2+4t+t﹣4=﹣t2+5t﹣4,
∴PF= ![]() (﹣t2+5t﹣4),
(﹣t2+5t﹣4),
∴S△PMN= ![]() (﹣t2+5t﹣4)2=
(﹣t2+5t﹣4)2= ![]() (t﹣4)2(t﹣1)2,
(t﹣4)2(t﹣1)2,
∵KAB=﹣1,∴∠OAB=45°,
∴CA=CN=4﹣t,
∴S△ACN= ![]() (t﹣4)2,
(t﹣4)2,
∵S△ACN=S△PMN,
∴ ![]() (t﹣4)2(t﹣1)2=
(t﹣4)2(t﹣1)2= ![]() (t﹣4)2,
(t﹣4)2,
∴t1=﹣1,(舍),t2=3,
∴M(3,3),
∵MX=NX=3,
∴N(3,1),
∴ON= ![]() ,
,
∵B(1,3),
∴OB= ![]() ,
,
∴OB=ON,∠OBN=∠ONB,
∵OB//MP
∴∠OBN=∠QPM,
∴∠ONB=∠QPM,∠RQA=45°,
∵∠MQR﹣∠BRN=45°,
∴∠BRN=∠MQP,
∴△BRN∽△MQP,
∴ ![]() ,
,
∵KPM=3,M(3,3),
∴lPM:y=3x﹣6,
∵lAB:y=﹣x+4,
∴P(2.5,1.5),
设R(3t,t),
∴Q(3t,﹣3t+4),
∴ ![]() ,
,
∴t1= ![]() ,t2=
,t2= ![]() (舍),
(舍),
∴R( ![]() ,
, ![]() ).
).
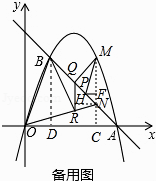
【解析】(1)利用已知得出A,B点坐标,进而利用待定系数法得出a,b的值;(2)已知MN=d,PF=t,由图可知MN=MF+FN,不妨将MF和FN用PF代替,即可得到MN与PF的关系:利用45°的直角三角形和平行线性质可推得FN=PF=t,∠MPF=∠BOD,再利用tan∠BOD=tan∠MPF,得 ![]() =
= ![]() =3,从而有MF=3PF=3t,从而得出d与t的函数关系;(3)过点N作NH⊥QR于点H,由图象可知R点横坐标为OC﹣HN,纵坐标为CN﹣RH.OC=OA﹣AC,其中OA已知,利用S△ACN=S△PMN求得AC=2t,再将用t表示的M点坐标代入抛物线解析式求得t值,即得AC的值,又由(2)中AC=CN,可知CN,则求得HN和RH的值是关键.根据tan∠HNR=tan∠NOC,可得
=3,从而有MF=3PF=3t,从而得出d与t的函数关系;(3)过点N作NH⊥QR于点H,由图象可知R点横坐标为OC﹣HN,纵坐标为CN﹣RH.OC=OA﹣AC,其中OA已知,利用S△ACN=S△PMN求得AC=2t,再将用t表示的M点坐标代入抛物线解析式求得t值,即得AC的值,又由(2)中AC=CN,可知CN,则求得HN和RH的值是关键.根据tan∠HNR=tan∠NOC,可得 ![]() =
= ![]() =
= ![]() ,设RH=n,HN=3n,勾股定理得出RN的值,再利用已知条件证得△PMQ∽△NBR,建立比例式求得n值,即可得出HN和RH的值,从而得到R的坐标.
,设RH=n,HN=3n,勾股定理得出RN的值,再利用已知条件证得△PMQ∽△NBR,建立比例式求得n值,即可得出HN和RH的值,从而得到R的坐标.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C. 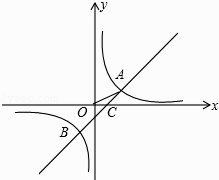
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简: ![]() (2)解方程:
(2)解方程:![]() .
.
【答案】(1) ![]() 或
或![]() ;(2)x=-2.
;(2)x=-2.
【解析】(1)先把括号内通分,再把除法转化为乘法,并把分子、分母分解因式约分化简;
(2)两边都乘以最简公分母2(x+3),把分式方程化为整式方程求解,求出x的值不要忘记检验.
(1)原式=![]() =
=![]() =
=![]() 或
或![]() ;
;
(2)解:去分母得:![]() ,
,
解得:x=﹣2,
经检验x=﹣2是分式方程的解,
∴原方程的解为x=﹣2
点睛:本题考查了分式的混合运算和解分式方程,熟练掌握分式的运算法则和解分式方程的方法是解答本题的关键.
【题型】解答题
【结束】
20
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中a= ;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为 ;
(4)若该辖区年龄在0~14岁的居民约有2400人,请估计该辖区居民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
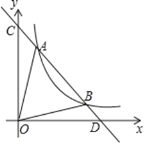
【题目】如图,一次函数![]() 分别交y轴、x轴于C、D两点,与反比例函数y=
分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出![]() <
<![]() 的x的取值范围;
的x的取值范围;
(3)求![]() 的面积.
的面积.
【答案】(1)y=![]() ;(2)
;(2) ![]() 或
或![]() ;(3)15.
;(3)15.
【解析】(1)把B(4,n)两点分别代入![]() 可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
(2)观察函数图象得到当![]() 或
或![]() ,反比例函数的图象在一次函数图象上方.
,反比例函数的图象在一次函数图象上方.
(3)求得直线![]() 与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
(1)将![]() 代入
代入![]() 得
得![]() ,
,
得反比例函数的关系式是![]() .
.
(2)![]() 或
或![]() ,
,
(3)![]() 点的坐标是(0,10),
点的坐标是(0,10),![]() 点的坐标是(5,0),
点的坐标是(5,0),
分别过点A、B两点作![]() 轴、
轴、![]() 轴的垂线段,
轴的垂线段,
![]() .
.
点睛:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及观察图象的能力.
【题型】解答题
【结束】
25
【题目】探索发现:![]() ;
;![]() ;
;![]() …根据你发现的规律,回答下列问题
…根据你发现的规律,回答下列问题
(1)![]() ,
,![]() ;
;
(2)利用你发现的规律计算:![]() ;
;
(3)灵活利用规律解方程:
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.
(1)求平均每分钟一个正门和一个侧门各可以通过多少名学生?
(2)检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用 6000 元购进一批衬衫,以 60 元/件的价格出售,很快售完,然后又用 13500元购进同款衬衫,购进数量是第一次的 2 倍,购进的单价比上一次每件多 5 元,服装店 仍按原售价 60 元/件出售,并且全部售完.
(1)该服装店第一次购进衬衫多少件?
(2)将该服装店两次购进衬衫看作一笔生意,那么这笔生意是盈利还是亏损?求出盈利(或 亏损)多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com