D
试题分析:由∠ABC=2∠C, BD平分∠ABC,可得∠ABD=∠DBC=∠C,则BD=DC,再有EB=AB,可得△ABD≌△EBD,△ABF≌△EBF即可得到AD=DE,∠BAF=∠BEA,从而可得(1)(2)正确;根据三角形外角的性质可得(3)正确;由AB=AG,EB=AB,可得EB=AG,证得EG=AH,即可得到(4)正确,即可得到结论.
∵∠ABC=2∠C, BD平分∠ABC,
∴∠ABD=∠DBC=∠C,
∴BD=DC,
∵EB=AB,
∴△ABD≌△EBD,△ABF≌△EBF,
∴AD=DE,∠BAF=∠BEA,
∴AC—BD=DE,
∴AC=BD+DE=2BF,
∵AD=DE,
∴∠DAF=∠DEA,
∵∠BEA=∠DAF+∠C,
∴∠BAE=∠AED+∠C,
∴∠BAE—∠C=∠AED,
∵AB=AG,EB=AB,
∴EB=AG,
EG=AH,
∵AG—AH=HG
∴BE—EG=HG,
4个全部正确,故选D.
考点:本题考查的是角平分线的性质,等腰三角形的性质,三角形外角的性质
点评:解答本题的关键是熟练掌握三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和.




 星级口算天天练系列答案
星级口算天天练系列答案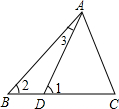 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.