
【题目】如图,已知抛物线![]() (b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b、c是常数,且c<0)与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
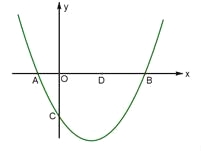
(1)b=______,点B的横坐标为_______(上述结果均用含c的代数式表示);
(2)连结BC,过点A作直线AE//BC,与抛物线交于点E.点D是x轴上一点,坐标为(2,0),当C、D、E三点在同一直线上时,求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方的抛物线上的一动点,连结PB、PC.设△PBC的面积为S.①求S的取值范围;②若△PBC的面积S为正整数,则这样的△PBC共有_____个.
【答案】(1)b=![]() +c;B的横坐标为-2c;(2)抛物线的解析式为y=
+c;B的横坐标为-2c;(2)抛物线的解析式为y=![]() x2-
x2-![]() x-2;(3)11.
x-2;(3)11.
【解析】试题本题是二次函数的综合题,其中涉及到运用待定系数法求一次函数、二次函数的解析式,二次函数的性质,直线平移的规律,求两个函数的交点坐标,三角形的面积,一元二次方程的根的判别及根与系数的关系等知识,综合性较强,有一定难度,运用数形结合、分类讨论及方程思想是解题的关键.
(1)将A(-1,0)代入y=![]() x2+bx+c,可以得出b=
x2+bx+c,可以得出b=![]() +c;根据一元二次方程根与系数的关系,得出-1xB=
+c;根据一元二次方程根与系数的关系,得出-1xB=![]() ,即xB=-2c;
,即xB=-2c;
(2)由y=![]() x2+bx+c,求出此抛物线与y轴的交点C的坐标为(0,c),则可设直线BC的解析式为y=kx+c,将B点坐标代入,运用待定系数法求出直线BC的解析式为y=
x2+bx+c,求出此抛物线与y轴的交点C的坐标为(0,c),则可设直线BC的解析式为y=kx+c,将B点坐标代入,运用待定系数法求出直线BC的解析式为y=![]() x+c;由AE∥BC,设直线AE得到解析式为y=
x+c;由AE∥BC,设直线AE得到解析式为y=![]() x+m,将点A的坐标代入,运用待定系数法求出直线AE得到解析式为y=
x+m,将点A的坐标代入,运用待定系数法求出直线AE得到解析式为y=![]() x+
x+![]() ;解方程组
;解方程组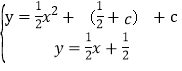 ,求出点E坐标为(1-2c,1-c),将点E坐标代入直线CD的解析式y=-
,求出点E坐标为(1-2c,1-c),将点E坐标代入直线CD的解析式y=-![]() x+c,求出c=-2,进而得到抛物线的解析式为y=
x+c,求出c=-2,进而得到抛物线的解析式为y=![]() x2-
x2-![]() x-2;
x-2;
(3)①分两种情况进行讨论:(Ⅰ)当-1<x<0时,由0<S<S△ACB,易求0<S<5;(Ⅱ)当0<x<4时,过点P作PG⊥x轴于点G,交CB于点F.设点P坐标为(x,![]() x2-
x2-![]() x-2),则点F坐标为(x,
x-2),则点F坐标为(x,![]() x-2),PF=PG-GF=-
x-2),PF=PG-GF=-![]() x2+2x,S=
x2+2x,S=![]() PFOB=-x2+4x=-(x-2)2+4,根据二次函数的性质求出S最大值=4,即0<S≤4,则0<S<5;
PFOB=-x2+4x=-(x-2)2+4,根据二次函数的性质求出S最大值=4,即0<S≤4,则0<S<5;
②由0<S<5,S为整数,得出S=1,2,3,4.分两种情况进行讨论:(Ⅰ)当-1<x<0时,根据△PBC中BC边上的高h小于△ABC中BC边上的高AC=![]() ,得出满足条件的△PBC共有4个;(Ⅱ)当0<x<4时,由于S=-x2+4x,根据一元二次方程根的判别式,得出满足条件的△PBC共有7个;则满足条件的△PBC共有4+7=11个.
,得出满足条件的△PBC共有4个;(Ⅱ)当0<x<4时,由于S=-x2+4x,根据一元二次方程根的判别式,得出满足条件的△PBC共有7个;则满足条件的△PBC共有4+7=11个.
试题解析:(1)b=c+![]() ,点B的横坐标为-2c.
,点B的横坐标为-2c.
(2)由y=![]() x2+(c+
x2+(c+![]() )x+c=
)x+c=![]() (x+1)(x+2c),设E(x,
(x+1)(x+2c),设E(x,![]() (x+1)(x+2c)).
(x+1)(x+2c)).
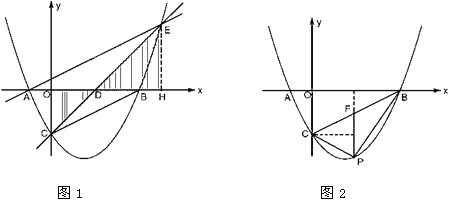
如图1,过点E作EH⊥x轴于H.
由于OB=2OC,当AE//BC时,AH=2EH.
所以x+1=(x+1)(x+2c).因此x=1-2c.所以E(1-2c,1-c).
当C、D、E三点在同一直线上时,![]() .所以
.所以![]() =
=![]() .
.
整理,得2c2+3c-2=0.解得c=-2或c=![]() (舍去).
(舍去).
所以抛物线的解析式为y=![]() x2-
x2-![]() x-2.
x-2.
(3)①当P在BC下方时,过点P作x轴的垂线交BC于F,如图2.
直线BC的解析式为y=![]() x-2.
x-2.
设P(m,![]() m2-
m2-![]() m-2),那么P(m,
m-2),那么P(m,![]() m-2),FP=-
m-2),FP=-![]() m2+2m.
m2+2m.
所以S△PBC=S△PBF+S△PCF=![]() FP(xB-xC)=2FP=-m2+4m=-(m-2)2+4.
FP(xB-xC)=2FP=-m2+4m=-(m-2)2+4.
因此当P在BC下方时,△PBC的最大值为4.
当P在BC上方时,因为S△ABC=5,所以S△PBC<5.
综上所述,0<S<5.
②若△PBC的面积S为正整数,则这样的△PBC共有11个.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
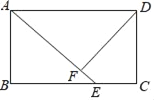
【题目】如图,已知矩形ABCD中,点E是BC边上的点,BE=2,EC=1,AE=BC,DF⊥AE,垂足为F.则下列结论:①△ADF≌△EAB;②AF=BE;③DF平分∠ADC;④sin∠CDF=![]() .其中正确的结论是_____.(把正确结论的序号都填上)
.其中正确的结论是_____.(把正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周六上午,小红到少年宫参加9点整开始的舞蹈表演.小红8点整从家步行出发,计划提前20min到达.小红步行了900m后发现一件道具忘在家里桌上,她立刻以原来速度的1.5倍沿原路返回,8点25分到达家中.
(1)求小红原来的步行速度.
(2)小红为确保不迟于8点40分到达少年宫,她拿到道具后,以12km/h的速度匀速骑自行车立即按原线路赶往少年宫.问小红在家最多只能耽搁多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育局为了了解初二学生第一学期参加社会实践活动的天数,随机抽查本市部分初二学生第一学期参加社会实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图)
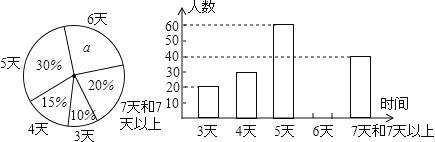
请你根据图中提供的信息,回答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)求实践天数为5天对应扇形的圆心角度数;
(4)如果该市有初二学生20000人,请你估计“活动时间不少于5天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
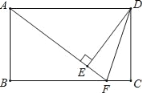
【题目】如图,已知矩形ABCD中,F是BC上一点,且AF=BC,DE⊥AF,垂足是E,连接DF.求证:
(1)△ABF≌△DEA;
(2)DF是∠EDC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
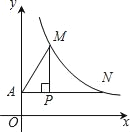
【题目】如图,过点P(2,![]() )作x轴的平行线交y轴于点A,交双曲线
)作x轴的平行线交y轴于点A,交双曲线![]() 于点N,作PM⊥AN交双曲线
于点N,作PM⊥AN交双曲线![]() 于点M,连接AM,若PN=4.
于点M,连接AM,若PN=4.
(1)求k的值;
(2)设直线MN解析式为y=ax+b,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
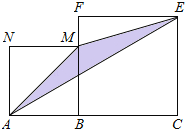
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
S3;则S3﹣S2= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com