练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．观察下列的“蜂窝图”

    则第n个图案中的“”的个数是3n+1．（用含有n的代数式表示）

    分析 根据题意可知：第1个图有4个图案，第2个共有7个图案，第3个共有10个图案，第4个共有13‘个图案，由此可得出规律．

    解答 解：由题意可知：每1个都比前一个多出了3个“”，
    ∴第n个图案中共有“”为：4+3（n-1）=3n+1
    故答案为：3n+1

    点评 本题考查学生的观察能力，解题的关键是熟练正确找出图中的规律，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．某市政府大力扶持大学生创业，李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯，销售过程中发现，每月销售量y（件）与销售单价x（元）之间可近似的看作一次函数：y=-10x+500．
    （1）李明每月获得利润为W（元），当销售单价定为多少元时，每月可获得最大利润？
    （2）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他的销售单价应该定在什么范围合适？他每月的成本最少需要多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，港口B在港口A的正东方向，一艘船从港口A出发，沿北偏东75°方向航行20海里到C处，此时测得港口B在C的南偏东45°方向，求C到港口B的距离，（结果保留到0.01海里）（参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．在平面直角坐标系xOy中，规定：抛物线y=a（x-h）2+k的伴随直线为y=a（x-h）+k．例如：抛物线y=2（x+1）2-3的伴随直线为y=2（x+1）-3，即y=2x-1．
    （1）在上面规定下，抛物线y=（x+1）2-4的顶点坐标为（-1，-4），伴随直线为y=x-3，抛物线y=（x+1）2-4与其伴随直线的交点坐标为（0，-3）和（-1，-4）；
    （2）如图，顶点在第一象限的抛物线y=m（x-1）2-4m与其伴随直线相交于点A，B（点A在点B的左侧），与x轴交于点C，D．
    ①若∠CAB=90°，求m的值；
    ②如果点P（x，y）是直线BC上方抛物线上的一个动点，△PBC的面积记为S，当S取得最大值$\frac{27}{4}$时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

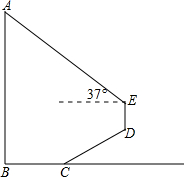    17．如图，某数学活动小组为测量学校旗杆AB的高度，沿旗杆正前方2$\sqrt{3}$米处的点C出发，沿斜面坡度i=1：$\sqrt{3}$的斜坡CD前进4米到达点D，在点D处安置测角仪，测得旗杆顶部A的仰角为37°，量得仪器的高DE为1.5米．已知A、B、C、D、E在同一平面内，AB⊥BC，AB∥DE．求旗杆AB的高度．（参考数据：sin37°≈$\frac{3}{5}$，cos37°≈$\frac{4}{5}$，tan37°≈$\frac{3}{4}$．计算结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

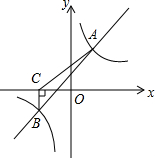    7．如图所示，一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A（2，4），B（-4，n）两点．
    （1）分别求出一次函数与反比例函数的表达式；
    （2）过点B作BC⊥x轴，垂足为点C，连接AC，求△ACB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

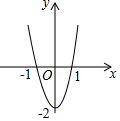    14．将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是（　　）
    A．y=（x-1）2+1B．y=（x+1）2+1C．y=2（x-1）2+1D．y=2（x+1）2+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．观察下表，回答问题：
    　4　3　5　32+42=52
    　6　8　10　62+82=102
    　8　15　17　82+152=172
    　10　24　26　102+242=262
    …………
    　60　x　y　602+x2=y2
    …………
    （1）数字60、x、y是第29行；
    （2）结合表格及相关知识，求x、y的值．

    查看答案和解析>>

    同步练习册答案