
【题目】如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
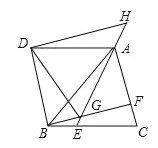
(1)求证:四边形DBCA是菱形.
(2)若菱形DBCA的面积为8![]() ,
,![]() ,求△DGH的面积.
,求△DGH的面积.
【答案】(1)四边形DBCA是菱形(证明过程见解析)(2)S△DGH=![]() .
.
【解析】
试题分析:(1)利用等边三角形的性质和折叠的定义,可知AC=AD=BC=BD,利用菱形的判定定理可得结论;
(2)首先证得△ABE≌△BCF(SAS),再由菱形的性质和全等三角形的判定证得△DBG≌△DAH(SAS),由全等三角形的性质和相似三角形的判定可证得△DBA∽△DGH,由相似三角形的性质面积比等于相似比的平方,可得结果.
试题解析:证明:∵△ABC是等边三角形,
∴AC=BC由折叠知AC=AD,BC=BD,
∴AC=AD=BC=BD,
∴四边形DBCA是菱形;
(2)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
在△ABE与△BCF中,
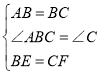 ,
,
∴△ABE≌△BCF(SAS),
∴∠AEB=∠BFC,
∵四边形DBCA是菱形,
∴DA∥BC,DB∥AC,∠BDA=∠C=60°,
∴∠HAD=∠AEB,∠DBG=∠BFC,
∴∠HAD=∠DBG,
在△DBG与△DAH中,
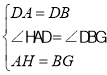 ,
,
∴△DBG≌△DAH(SAS),
∴DG=DH,∠BDG=∠ADH,
∴∠HDG=∠ADH+∠GDA=∠BDG+∠GDA=∠BDA=60°,
又∵DA=DB,DG=DH,
∴△DBA∽△DGH,
∴![]() ,
,
∵S△DBA=![]() S菱形DBCA=
S菱形DBCA=![]() ,
,
∴S△DGH=![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.
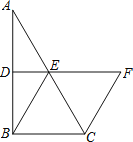
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
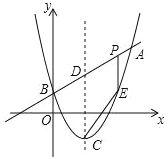
(1)求m的值和该二次函数的表达式.为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(3)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
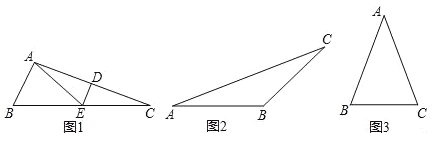
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.
(2)如图2,已知△ABC是特异三角形,且∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
(3)如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形的两边长分别为5和6,第三边的长是方程(x-1)(x-4)=0的根,则这个三角形的周长是( )
A. 15 B. 12 C. 15或12 D. 以上选项都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解09届本科生的就业情况,今年3月,某网站对09届本科生的签约状况进行了网络调查.截至3月底,参与网络调查的12 000人中,只有4320人已与用人单位签约.在这个网络调查中,样本容量是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com