
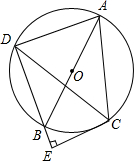
 如图,在Rt△ABC中,BC=5cm,AC=12cm,以AB长为直径作圆⊙O,作弦CD=AC,CE⊥DB的延长线于点E.
如图,在Rt△ABC中,BC=5cm,AC=12cm,以AB长为直径作圆⊙O,作弦CD=AC,CE⊥DB的延长线于点E.分析 (1)利用CA=CD得到∠CDA=∠CAD,再根据圆周角定理得到∠CDA=∠ABC,所以∠ABC=∠CAD;
(2)连接OC,如图,利用圆周角定理得到∠EBC=∠ABC,再证明∠EBC=∠OCB,则可判定OC∥DE,然后利用CE⊥BC得到CE⊥OC,则可根据切线的判定可得到CE是⊙O的切线.
解答 证明:(1)∵CA=CD,
∴∠CDA=∠CAD,
∵∠CDA=∠ABC,
∴∠ABC=∠CAD;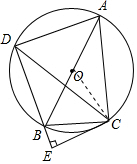
(2)连接OC,如图,
∵∠EBC=∠CAD,∠ABC=∠CAD,
∴∠EBC=∠ABC,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠EBC=∠OCB,
∴OC∥DE,
∵CE⊥BC,
∴CE⊥OC,
∴CE是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了圆周角定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 购进甲种服装的数量/件 | 10 | 20 | x |
| 购进甲种服装所用费用/元 | 800 | 1600 | 80x |
| 购进乙种服装所用费用/元 | 5400 | 4800 | 6000-60x |
| 购进甲种服装的数量/件 | 10 | 20 | x |
| 甲种服装获得的利润/元 | 400 | 800 | 40x |
| 乙种服装获得的利润/元 | 2700 | 2400 | 3000-30x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com