
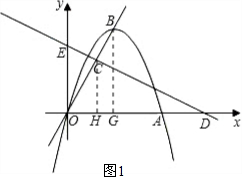
 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上. 的解析式;
的解析式; ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
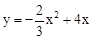 ;(2)①
;(2)①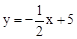 ;②(-5,
;②(-5,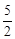 )或(4,8)或
)或(4,8)或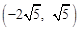 .
. 的顶点B(m,6)在直线
的顶点B(m,6)在直线 上可求出m的值,再用待定系数发即可求出此抛物线的解析式.
上可求出m的值,再用待定系数发即可求出此抛物线的解析式. 上,∴m="3." ∴B(3,6).
上,∴m="3." ∴B(3,6).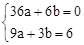 ,解得
,解得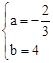 .
.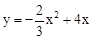 .
.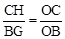 .
.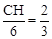 ,即CH="4." ∴点C的坐标为(2,4).
,即CH="4." ∴点C的坐标为(2,4).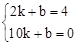 ,解得:
,解得: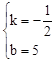 .
.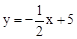 .
.
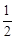 OE=
OE=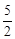 . ∴NK=
. ∴NK=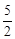 .
.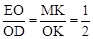 .∴OK=5.∴N1(-5,
.∴OK=5.∴N1(-5,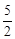 ).
).
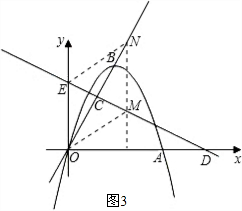
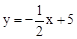 ,∴E(0,5).
,∴E(0,5).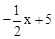 ),
),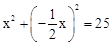 ,解得x=
,解得x=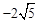 .∴M
.∴M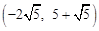 .
.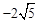 ,y),则
,y),则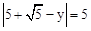 ,解得y=
,解得y=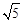 或y=
或y=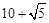 (舍去).∴N3
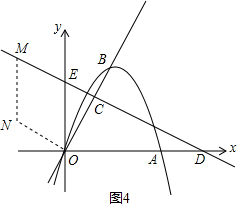
(舍去).∴N3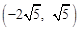 .
.
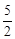 )或(4,8)或
)或(4,8)或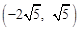 .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”. 的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com