
【题目】如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正确结论有( )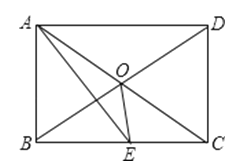
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=30°,
∵OA=OD,
∴∠ODA=∠DAC=30°,
∴∠DOC=60°,
∵OD=OC,
∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°
∴∠DAC=∠ACB=30°,
∴AC=2AB,
∵AC>BC,
∴2AB>BC,∴②错误;
∵AD∥BC,
∴∠DBC=∠ADB=30°,
∵AE平分∠DAB,∠DAB=90°,
∴∠DAE=∠BAE=45°,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠AEB=∠BAE,
∴AB=BE,
∵四边形ABCD是矩形,
∴∠DOC=60°,DC=AB,
∵△DOC是等边三角形,
∴DC=OD,
∴BE=BO,
∴∠BOE=∠BEO=![]() (180°﹣∠OBE)=75°,
(180°﹣∠OBE)=75°,
∵∠AOB=∠DOC=60°,
∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,
∴根据等底等高的三角形面积相等得出S△AOE=SCOE , ∴④正确;
故选C.
【考点精析】认真审题,首先需要了解等边三角形的判定(三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形),还要掌握含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】观察某月日历,回答下列问题:
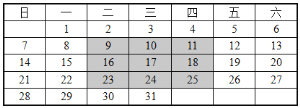
![]() 观察图中的阴影部分的
观察图中的阴影部分的![]() 个数,你知道他们之间有什么关系吗?写出你认为正确的一个结论;
个数,你知道他们之间有什么关系吗?写出你认为正确的一个结论;
![]() 小强一家外出游玩了
小强一家外出游玩了![]() 天,这
天,这![]() 天的日期之和是
天的日期之和是![]() ,小强一家几号外出的?
,小强一家几号外出的?
![]() 像上面第
像上面第![]() 题那样现在要用一个方框去框该月历上的九个数,这九个数的和可能是
题那样现在要用一个方框去框该月历上的九个数,这九个数的和可能是![]() 吗?如果不能,请说明理由;如果能,请求出框出的这九个数.
吗?如果不能,请说明理由;如果能,请求出框出的这九个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
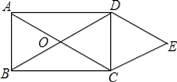
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形.
(2)若AB=6,BC=8,求四边形OCED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC. 如果AC=3,则PD的长为______________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
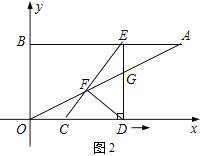
【题目】如图1,已知点A(8,4),点B(0,4),线段CD的长为3,点C与原点O重合,点D在x轴正半轴上.线段CD沿x轴正方向以每秒1个单位长度的速度向右平移,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F(如图2),设运动时间为t.当E点与A点重合时停止运动.
(1)求线段CE的长;
(2)记△CDE与△ABO公共部分的面积为S,求S关于t的函数关系式;
(3)如图2,连接DF.
①当t取何值时,以C、F、D为顶点的三角形为等腰三角形?
②△CDF的外接圆能否与OA相切?如果能,直接写出此时t的值;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有( )千米到达甲地.
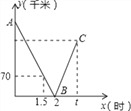
A. 70 B. 80 C. 90 D. 100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点D在边BC上
,点D在边BC上![]() 与B、C不重合
与B、C不重合![]() ,四边形ADEF为正方形,过点F作
,四边形ADEF为正方形,过点F作![]() ,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:![]() ;
;![]() :
:![]() :2;
:2;![]() ;
;
其中正确的结论的个数是![]()

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.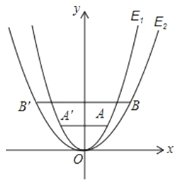
(1)求m的值;
(2)求抛物线E2所表示的二次函数的表达式;
(3)在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com