
【题目】如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3 ![]() ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( ) 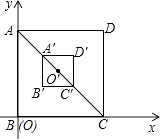
A.![]()
B.![]()
C.![]()
D.![]()
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】大润发超市在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,超市应将这种商品的售价定为多少?
(2)设每件商品的售价为x元,超市所获利润为y元. ①求y与x之间的函数关系式;
②物价局规定该商品的售价不能超过40元/件,超市为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图①,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,请直接写出线段BE与线段CD的数量关系: ;
(2)操作探究
如图②,将图①中的△ABC绕点A顺时针旋转,旋转角为α(0<α<360),请判断线段BE与线段CD的数量关系,并说明理由.
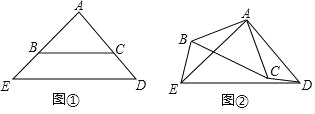
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?
(2)某蔬菜公司的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司的加工生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案:
方案一:将蔬菜全部进行粗加工.
方案二:尽可能多地对蔬菜进行精加工,没来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE. 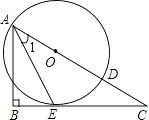
(1)求证:AE平分∠CAB;
(2)探求图中∠1与∠C的数量关系,并求当AE=EC时tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如图①,若点B把线段分成两条长度相等的线段AB和BC,则点B叫做线段AC的中点.
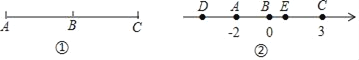
回答问题:
(1)如图②,在数轴上,点A所表示的数是﹣2,点B所表示的数是0,点C所表示的数是3.
①若A是线段DB的中点,则点D表示的数是 ;
②若E是线段AC的中点,求点E表示的数.
(2)在数轴上,若点M表示的数是m,点N所表示的数是n,点P是线段MN的中点.
①若点P表示的数是1,则m、n可能的值是 (填写符合要求的序号);
(i)m=0,n=2;(ii)m=﹣5,n=7;(iii)m=0.5,n=1.5;(iv)m=﹣1,n=2
②直接用含m、n的代数式表示点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
![]()
A. 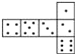 B.
B. 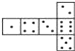 C.
C.  D.
D. 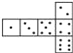
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com