Question

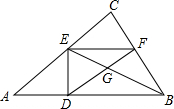
1．如图所示，在Rt△ABC中，∠C=90°，AC=4，BC=3，AB上有一动点D以每秒4个单位的速度从点A向点B运动，当点D运动到点B时停止运动．过点D作DE⊥AB，垂足为点D，过点E作EF∥AB交BC于点F，连接BE交DF于点G，设点D运动的时间为t，当S_△BDG=4S_△EFG时，t的值为（　　）

• A． t=$\frac{14}{17}$
• B． t=$\frac{12}{10}$
• C． t=$\frac{10}{17}$
• D． t=$\frac{8}{17}$

Answer 1

分析 首先求出AB，由△ADE∽△ACB，求出AE=5t，DE=3t，EC=4-5t，再根据EF∥AB，得$\frac{EC}{AC}$=$\frac{EF}{AB}$，求出EF，由EF∥DB，推出△EGF∽△BGD，得$\frac{{S}_{△EGF}}{{S}_{△BDG}}$=（$\frac{EF}{DB}$）²=$\frac{1}{4}$，推出DB=2EF，列出方程即可解决问题．

解答 解：在Rt△ABC中，∵∠C=90°，AC=4，BC=3，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5，
∵∠A=∠A，∠EDA=∠C=90°，
∴△ADE∽△ACB，
∴$\frac{AD}{AC}$=$\frac{DE}{CB}$=$\frac{AE}{BC}$，
∵AD=4t，
∴AE=5t，DE=3t，
∴EC=4-5t，
∵EF∥AB，
∴$\frac{EC}{AC}$=$\frac{EF}{AB}$，
∴$\frac{4-5t}{4}$=$\frac{EF}{5}$，
∴EF=$\frac{5}{4}$（4-5t），
∵EF∥DB，
∴△EGF∽△BGD，
∴$\frac{{S}_{△EGF}}{{S}_{△BDG}}$=（$\frac{EF}{DB}$）²=$\frac{1}{4}$，
∴BD=2EF，
∴5-4t=$\frac{5}{4}$（4-5t），
∴t=$\frac{10}{17}$．
故选C．

点评 本题考查三角形综合题-动点问题、相似三角形的判定和性质．平行线的性质等知识，解题的关键是利用相似三角形的性质，解决问题，学会利用方程的思想思考问题，属于中考常考题型．