
【题目】在四边形 ABCD 中,E 为 BC 边中点.
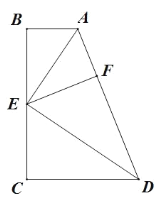
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD
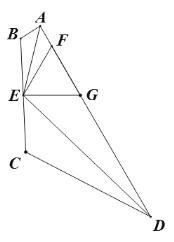
(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.
【答案】(Ⅰ)(1)证明见解析;(2)证明见解析;(Ⅱ)(1)证明见解析;(2)证明见解析.
【解析】
(Ⅰ)(1)运用SAS证明△ABE≌AFE即可;
(2)由(1)得出∠AEB=∠AEF,BE=EF,再证明△DEF≌△DEC(SAS),得出DF=DC,即可得出结论;
(Ⅱ)(1)同(Ⅰ)(1)得△ABE≌△AFE(SAS),△DGE≌△DCE(SAS),由全等三角形的性质得出BE=FE,∠AEB=∠AEF,CE=GE,∠CED=∠GED,进而证明△EFG是等边三角形;
(2)由△EFG是等边三角形得出GF=EE=BE=![]() BC,即可得出结论.
BC,即可得出结论.
(Ⅰ)(1)∵AE平分∠BAD,
∴∠BAE=∠FAE,
在△ABE和△AFE中,
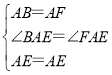 ,
,
∴△ABE≌△AFE(SAS),
(2)∵△ABE≌△AFE,
∴∠AEB=∠AEF,BE=EF,
∵E为BC的中点,
∴BE=CE,
∴FE=CE,
∵∠AED=∠AEF+∠DEF=90°,
∴∠AEB+∠DEC=90°,
∴∠DEF=∠DEC,
在△DEF和△DEC中,
 ,
,
∴△DEF≌△DEC(SAS),
∴DF=DC,
∵AD=AF+DF,
∴AD=AB+CD;
(Ⅱ)(1)∵E为BC的中点,
∴BE=CE=![]() BC,
BC,
同(Ⅰ)(1)得:△ABE≌△AFE(SAS),
△DEG≌△DEC(SAS),
∴BE=FE,∠AEB=∠AEF,CE=GE,∠CED=∠GED,
∵BE=CE,
∴FE=GE,
∵∠AED=120°,∠AEB+∠CED=180°-120°=60°,
∴∠AEF+∠GED=60°,
∴∠GEF=60°,
∴△EFG是等边三角形,
(2)∵△EFG是等边三角形,
∴GF=EF=BE=![]() BC,
BC,
∵AD=AF+FG+GD,
∴AD=AB+CD+![]() BC.
BC.


科目:初中数学 来源: 题型:
【题目】如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘.
(1)转动甲转盘,指针指向的数字小于3的概率是 ;
(2)同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
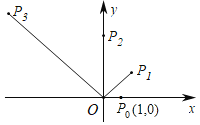
【题目】如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按照逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按照逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P8的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法正确的有( )
①正八边形的每个内角都是135°;
②反比例函数y=﹣![]() ,当x<0时,y随x的增大而增大;
,当x<0时,y随x的增大而增大;
③长度等于半径的弦所对的圆周角为30°;
④分式方程![]() 的解为
的解为![]() ;
;
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在AB上,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.
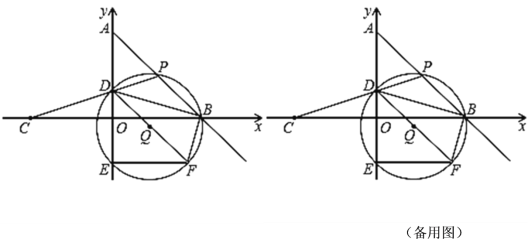
(1)求直线AB的函数解析式;
(2)求证:∠BDE=∠ADP;
(3)设DE=x,DF=y.请求出y关于x的函数解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,以AB为直径作半圆O,半径OA绕点O顺时针旋转得到OC,点A的对应点为C,当点C与点B重合时停止.连接BC并延长到点D,使得CD=BC,过点D作DE⊥AB于点E,连接AD,AC.

(1)AD= ;
(2)如图1,当点E与点O重合时,判断△ABD的形状,并说明理由;
(3)如图2,当OE=1时,求BC的长;
(4)如图3,若点P是线段AD上一点,连接PC,当PC与半圆O相切时,直接写出直线PC与AD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如果α,β都为锐角,且tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
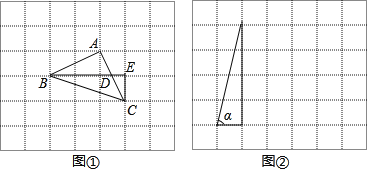
解决:如图①,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,连结AC,易证△ABC是等腰直角三角形,因此可求得α+β=∠ABC= .
拓展:参考以上方法,解决下列问题:如果α,β都为锐角,当tanα=4,tanβ=![]() 时,
时,
(1)在图②的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β;
(2)求出α﹣β= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,把它内部及边上的横、纵坐标均为整数的点称为整点,点P为抛物线![]() 的顶点(m为整数),当点P在正方形OABC内部或边上时,抛物线下方(包括边界)的整点最少有( )
的顶点(m为整数),当点P在正方形OABC内部或边上时,抛物线下方(包括边界)的整点最少有( )

A.3个B.5个C.10个D.15个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com