
【题目】在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为 ![]() 个单位长度/秒,则2017秒时,点P的坐标是( )
个单位长度/秒,则2017秒时,点P的坐标是( ) 
A.(2017,0)
B.(2017, ![]() )
)
C.(2017,﹣ ![]() )
)
D.(2016,0)
【答案】B
【解析】解:设第n秒运动到Pn(n为自然数)点, 观察,发现规律:P1(1, ![]() ),P2(2,0),P3(3,﹣
),P2(2,0),P3(3,﹣ ![]() ),P4(4,0),P5(5,
),P4(4,0),P5(5, ![]() ),…,
),…,
∴P4n+1(4n+1, ![]() ),P4n+2(4n+2,0),P4n+3(4n+3,﹣
),P4n+2(4n+2,0),P4n+3(4n+3,﹣ ![]() ),P4n+4(4n+4,0).
),P4n+4(4n+4,0).
∵2017=4×504+1,
∴P2017为(2017, ![]() ).
).
故选B.
设第n秒运动到Pn(n为自然数)点,根据点P的运动规律找出部分Pn点的坐标,根据坐标的变化找出变化规律“P4n+1(4n+1, ![]() ),P4n+2(4n+2,0),P4n+3(4n+3,﹣
),P4n+2(4n+2,0),P4n+3(4n+3,﹣ ![]() ),P4n+4(4n+4,0)”,依此规律即可得出结论.
),P4n+4(4n+4,0)”,依此规律即可得出结论.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
(1)当点P与点Q重合时,如图1,写出QE与QF的数量关系,不证明;
(2)当点P在线段AB上且不与点Q重合时,如图2,(1)的结论是否成立?并证明;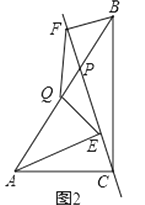
(3)当点P在线段BA(或AB)的延长线上时,如图3,此时(1)的结论是否成立?请画出图形并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点. 
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是4,求线段BF的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校2017年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元;
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)2018年这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2910元,那么这所学校最多可购买多少个乙种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( ) 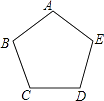
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC=5,BC=6(如图所示),将△ABC沿射线BC方向平移m个单位得到△DEF,顶点A、B、C分别与D、E、F对应.若以点A、D、E为顶点的三角形是等腰三角形,且AE为腰,则m的值是 . 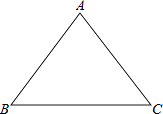
查看答案和解析>>
科目:初中数学 来源: 题型:
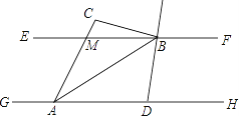
【题目】如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
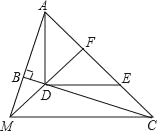
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com