
分析 (1)根据异分母分式加减法运算法则计算;
(2)根据异分母分式加减法运算法则计算;
(3)根据异分母分式加减法运算法则计算;
(4)根据异分母分式加减法运算法则计算;
(5)根据异分母分式加减法运算法则计算;
(6)根据分式的通分法则和约分法则进行计算即可.
解答 解:(1)$\frac{y}{4x}$-$\frac{x}{6y}$=$\frac{3{y}^{2}-2{x}^{2}}{12xy}$;
(2)$\frac{1}{a-2}$+$\frac{1}{a+2}$=$\frac{a+2}{{a}^{2}-4}$+$\frac{a-2}{{a}^{2}-4}$=$\frac{2a}{{a}^{2}-4}$;
(3)$\frac{2}{{x}^{2}-2x}$-$\frac{1}{x-2}$=$\frac{2}{x(x-2)}-\frac{x}{x(x-2)}$=-$\frac{1}{x}$;
(4)$\frac{2a}{{a}^{2}-9}$-$\frac{2}{3+a}$=$\frac{2a}{(a+3)(a-3)}$-$\frac{2(a-3)}{(a+3)(a-3)}$=$\frac{6}{{a}^{2}-9}$;
(5)$\frac{1}{a-4}$-$\frac{2}{a+4}$-$\frac{8}{{a}^{2}-16}$=$\frac{a+4}{{a}^{2}-16}$-$\frac{2(a-4)}{{a}^{2}-16}$-$\frac{8}{{a}^{2}-16}$=-$\frac{1}{a+4}$;
(6)($\frac{x}{x-2}$-$\frac{x}{x+2}$)÷$\frac{4x}{2-x}$=$\frac{4x}{(x+2)(x-2)}$×$\frac{2-x}{4x}$=-$\frac{1}{x+2}$.
点评 本题考查的是分式的混合运算,掌握分式的通分法则和约分法则是解题的关键.


科目:初中数学 来源: 题型:填空题
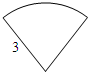 如图,半径为3cm的扇形纸片的周长为10cm,将它围成一个圆锥的侧面,则圆锥的底面圆的半径等于$\frac{2}{π}$cm.(结果保留π)
如图,半径为3cm的扇形纸片的周长为10cm,将它围成一个圆锥的侧面,则圆锥的底面圆的半径等于$\frac{2}{π}$cm.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-(x-1)2-2 | B. | y=-(x-1)2+2 | C. | y=-(x+1)2-2 | D. | y=-(x+1)2-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
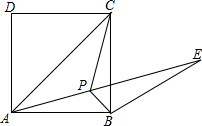 如图,已知点P为正方形ABCD内一点,∠BAP=∠BCP=15°.
如图,已知点P为正方形ABCD内一点,∠BAP=∠BCP=15°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )| A. | 70° | B. | 40° | C. | 35° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
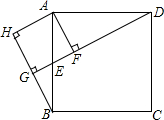 如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.
如图,在正方形ABCD中,点E是边AB的中点,过点A作DE的垂线,垂足为F,过点B作DE的垂线,垂足为G,过点A作BG的垂线,垂足为H.求证:四边形AFGH是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
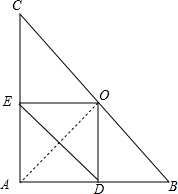 如图,在Rt△ABC中,AB=AC,∠BAC=90°,点O为BC的中点,点D,E分别在AB,AC上滑动且保持BD=AE.在滑动过程中△ODE与△ABC会相似吗?会永远相似吗?请说明你的结论.
如图,在Rt△ABC中,AB=AC,∠BAC=90°,点O为BC的中点,点D,E分别在AB,AC上滑动且保持BD=AE.在滑动过程中△ODE与△ABC会相似吗?会永远相似吗?请说明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
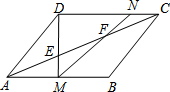 平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.
平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com