
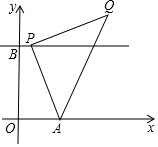
 如图,在平面直角坐标系中,A(1,0),B(0,2),过点B作直线l∥x轴,点P(a,2)是直线l上的动点,以AP为边在AP右侧作等腰Rt△APQ,使∠APQ=Rt∠.
如图,在平面直角坐标系中,A(1,0),B(0,2),过点B作直线l∥x轴,点P(a,2)是直线l上的动点,以AP为边在AP右侧作等腰Rt△APQ,使∠APQ=Rt∠.分析 (1)①证明△BQM≌△ABO,得出BM=AO=1,QM=BO=2,求出OM=3,即可得出结果;
②由最短路径问题求出点A关于y轴的对称点,由勾股定理求出DQ的长,用待定系数法求出直线DQ的解析式,即可得出点C的坐标;
(2)证明三角形全等同(1),即可得出结果.
解答 解: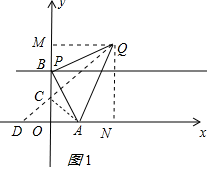 (1)①a=0时,P与B重合,如图1所示:
(1)①a=0时,P与B重合,如图1所示:
作QM⊥y轴于M,
∵A(1,0),B(0,2),
∴AO=1,BO=2,
∵△APQ是等腰直角三角形,
∴∠ABQ=90°,BA=BQ,由角的互余关系得:∠ABO=∠BQM,
在△BQM和△ABO中,$\left\{\begin{array}{l}{∠QMB=∠BOA=90°}&{\;}\\{∠BQM=∠ABO}&{\;}\\{BQ=BA}&{\;}\end{array}\right.$,
∴△BQM≌△ABO(AAS),
∴BM=AO=1,QM=BO=2,
∴OM=3,
∴点Q的坐标是(2,3);
故答案为:(2,3);
②作点A关于y轴的对称点D(-1,0),连接DQ交y轴于C,
此时CA=CD,CA+CQ的值最小,CA+CQ=DQ=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
即CA+CQ的最小值为3$\sqrt{2}$;
设直线DQ的解析式为y=kx+b,
根据题意得:$\left\{\begin{array}{l}{2k+b=3}\\{-k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线DQ的解析式为y=x+1,
当x=0时,y=1,
∴点C的坐标为(0,1);
故答案为:3$\sqrt{2}$,(0,1);
(2)如图2所示:作AE⊥BP,QF⊥BP,同(1)①得:△APE≌△PQF,
∴PE=FQ=BP-BE=3-1=2,AE=PF=2,
∴BF=3+2=5,
∴点Q的坐标为(5,0).
点评 本题是三角形综合题目,考查了全等三角形的判定与性质、勾股定理、最短路径问题、轴对称的性质、待定系数法求直线的解析式等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
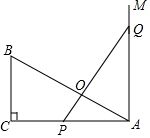 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E,则下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E,则下列结论错误的是( )| A. | BD+ED=BC | B. | ED+AC>AD | C. | DA平分∠EDC | D. | DE平分∠ADB |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
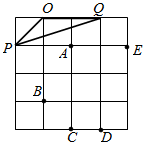 如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.
如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
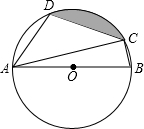 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.
如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com