
【题目】在平面直角坐标系中,点A(a,0),点B(2﹣a,0),且A在B的左边,点C(1,﹣1),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )
A. ﹣1<a≤0B. 0≤a<1C. ﹣1<a<1D. ﹣2<a<2
【答案】A
【解析】
根据“点A(a,0),点B(2-a,0),且A在B的左边,点C(1,-1),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个”,得出除了点C外,其它三个横纵坐标为整数的点落在所围区域的边界上,即线段AB上,从而求出a的取值范围.
∵点A(a,0)在点B(2-a,0)的左边,∴ a<2-a,解得:a<1,记边AB,BC,AC所围成的区域(含边界)为区域M,则落在区域M的横纵坐标都为整数的点个数为4个.
∵点A,B,C的坐标分别是(a,0),(2-a,0),(1,-1),∴区域M的内部(不含边界)没有横纵坐标都为整数的点,∴已知的4个横纵坐标都为整数的点都在区域M的边界上.
∵点C(1,-1)的横纵坐标都为整数且在区域M的边界上,∴其他的3个都在线段AB上,∴![]() .
.
解得:![]() .
.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,![]() ABCD绕点A逆时针旋转30°,得到
ABCD绕点A逆时针旋转30°,得到![]() AB′C′D′,若点B′与点B是对应点,若点B′恰好落在BC边上,则∠C=( )
AB′C′D′,若点B′与点B是对应点,若点B′恰好落在BC边上,则∠C=( )
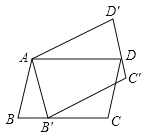
A. 105°B. 120°C. 135°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下列空格完成证明:如图, EF∥AD , 1 2 , BAC 70 ,求AGD .
解:∵ EF∥AD ,
∴ 2 .( )
∵ 1 2 ,
∴ 1 3.( )
∴ ∥ .( )
∴ BAC 180 .( )
∵ BAC 70 ,
∴ AGD .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,∠ADB=∠BAC,BE平分∠ABC,过点E作EF/AD,交BC于点F

(1)求证:∠BAD=∠C;
(2)若∠C=20°,∠BAC=110°,求∠BEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABED是正方形,DB⊥BC,点E为线段DC的中点,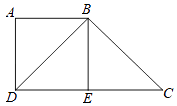
(1)求证:BD2=ADDC.
(2)连接AE,求证:ABCE为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款456万元购进A,B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表:
单价/万元 | 工作效率/(只/h) | |
A种型号 | 16 | 4000 |
B种型号 | 14.8 | 3000 |
(1)求购进A,B两种型号的口罩生产线各多少台.
(2)现有200万只口罩的生产任务,计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h,则至少租用A种型号的口罩机多少台才能在5天内完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD,BC=BD,若∠ABD=![]() ∠BAC=,则∠BDC的度数为( )
∠BAC=,则∠BDC的度数为( )

A. 2B. 45°+![]() C. 90°-D. 180°-3
C. 90°-D. 180°-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com