
【题目】如图1,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC. 
(1)判断△AOG的形状,并予以证明;
(2)若点B、C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图2,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标. 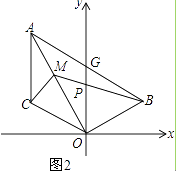
【答案】
(1)解:△AOG的形状是等腰三角形,
理由如下:
∵AC∥y轴,
∴∠CAO=∠GOA,
∵AO平分∠BAC,
∴∠CAO=∠GAO,
∴∠GOA=∠GAO,
∴AG=OG,
∴△AOG是等腰三角形
(2)解:如图1,接连BC,过O作OE⊥AB于E,过点C作CD⊥x轴于点D,
∵B、C关于y轴对称,AC∥y轴,
∴AC⊥BC,
在Rt△COD和Rt△BOE中,
![]() ,
,
∴△COD≌△BOE(HL),
∴∠DCO=∠EBO,
∴∠BAC+∠BOC=180°,
设∠BAO=∠CAO=x,∠OBC=∠OCB=y,
∴2x+∠BOC=180°,
又∵2y+∠BOC=180°,
∴x=y,故∠OAC=∠OBC,
∴∠AOB=∠ACB=90°,
∴AO⊥OB
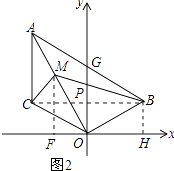
(3)解:如图2,连BC,作MF⊥x轴于F,BH⊥x轴于H,
则∠ACB=90°,
∵∠ACM=45°,
∴CM平分∠ACB,又AM平分∠BAC,
∴BM平分∠ABC,设∠ABM=∠CBM=z,
由(2)可得∠OMB=x+z,∠OBM=y+z=x+z
∴∠OMB=∠OBM,
∴OM=OB
∴△OBM为等腰直角三角形,
∵ 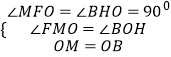 ,
,
∴△OMF≌△OBH(AAS),
∴OF=BH=1,MF=OH=3,
∴M(﹣1,3)
【解析】(1)△AOG的形状是等腰三角形,利用已知条件证明AG=OG即可;(2)接连BC,易证△COD≌△BOE(HL),设∠BAO=∠CAO=x,∠OBC=∠OCB=y,利用全等三角形的性质和已知条件证明∠AOB=∠ACB=90°,即可得到AO⊥BO;(3)连BC,作MF⊥x轴于F,BH⊥x轴于H,易证△OMF≌△OBH,OF=BH=1,MF=OH=3,所以M(﹣1,3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC, 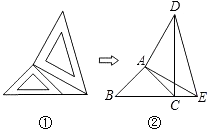
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】存折现有5000元,如果存入记为正,支取为负,上半年某人支存情况为+500元,-300元,+1200元,-600元,则该人现有存款为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
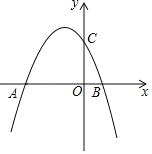
【题目】如图,已知抛物线y=-![]() x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
(1)求该抛物线的解析式;
(2)写出顶点的坐标,并求AB的长;
(3)若点A,O,C均在⊙D上,请写出点D的坐标,连接BC,并判断直线BC与⊙D的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
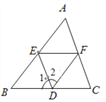
【题目】如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com