
 <1,且b2-4ac>0,再由不等式的基本性质可求出a的取值范围,再根据a、b、c之间的关系即可求解.
<1,且b2-4ac>0,再由不等式的基本性质可求出a的取值范围,再根据a、b、c之间的关系即可求解. <1,且b2-4ac>0①,
<1,且b2-4ac>0①, +1,可得(
+1,可得( -
- )2>1,
)2>1, >
> +1,故a>4,
+1,故a>4, ≥2
≥2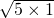 >4,分别取a、b、c的最小整数5、5、1.
>4,分别取a、b、c的最小整数5、5、1. <1,且b2-4ac>0得到关于a、b、c的关系式是解答此题的关键.
<1,且b2-4ac>0得到关于a、b、c的关系式是解答此题的关键. 

 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
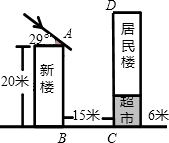 夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)查看答案和解析>>
科目:初中数学 来源: 题型:
| 13 |
| 2 |
| 9 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com