

分析 (1)根据矩形的性质,对边相等建立方程求解即可;
(2)分两种情况,利用平行四边形的性质对边相等建立方程求解即可得出结论;
(3)先由平行四边形建立方程求出时间,再判定邻边是否相等,判断出不能是菱形,设出点Q的运动速度,用菱形的性质建立方程求解即可求出速度.
解答 解:(1)∵∠ABC=90°,AP∥BQ,
∴当AP=BQ时,四边形ABQP成为矩形,
由运动知,AP=t,CQ=3t,
∴BQ=22-3t,
∴t=22-3t,解得t=$\frac{11}{2}$.
∴当t=$\frac{11}{2}$时,四边形ABQP成为矩形;
(2)∵当P、Q两点与A、B两点构成的四边形是平行四边形时,就是(1)中的情形,此时t=$\frac{11}{2}$.
当P、Q两点与C、D两点构成的四边形是平行四边形时,
∵PD∥QC,
∴当PD=QC时,四边形PQCD为平行四 边形.
此时,16-t=3t,t=4;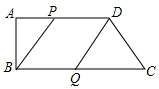 故当t=或t=4时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形.
故当t=或t=4时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形.
(3)四边形PBQD不能成为菱形.理由如下:
∵PD∥BQ,
∴当PD=BQ=BP时,四边形PBQD能成为菱形.
由PD=BQ,得16-t=22-3t,解得t=3,
当t=3时,PD=BQ=13,AP=AD-PD=16-13=3.
在Rt△ABP中,AB=8,根据勾股定理得,BP═$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{64+9}$=$\sqrt{73}$≠13
∴四边形PBQD不能成为菱形;
如果Q点的速度改变为vcm/s时,能够使四边形PBQD在时刻ts为菱形,
由题意得,$\left\{\begin{array}{l}{16-t=22-vt}\\{16-t=\sqrt{64+{t}^{2}}}\end{array}\right.$,解得,$\left\{\begin{array}{l}{t=6}\\{v=2}\end{array}\right.$.
故点Q的速度为2cm/s时,能够使四边形PBQD在某一时刻为菱形.
点评 此题是四边形综合题,主要考查了平行四边形的性质,矩形的性质,菱形的性质,解本题的关键是用方程(组)的思想解决问题,是一道中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
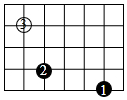 如图,在围棋盘上有三枚棋子,如果黑棋①的位置用有序数对(0,-1)表示,黑棋②的位置用有序数对(-3,0)表示,则白棋③的位置可用有序数对( )表示.
如图,在围棋盘上有三枚棋子,如果黑棋①的位置用有序数对(0,-1)表示,黑棋②的位置用有序数对(-3,0)表示,则白棋③的位置可用有序数对( )表示.| A. | (-2,4) | B. | (2,-4) | C. | (4,-2) | D. | (-4,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
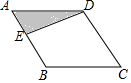 如图,点E为菱形ABCD边上的一个动点,并延A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,则下列图象能大致反映y与x的函数关系的是( )
如图,点E为菱形ABCD边上的一个动点,并延A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,则下列图象能大致反映y与x的函数关系的是( )| A. | 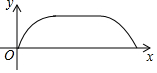 | B. | 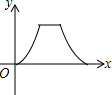 | ||
| C. | 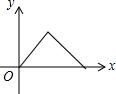 | D. | 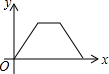 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
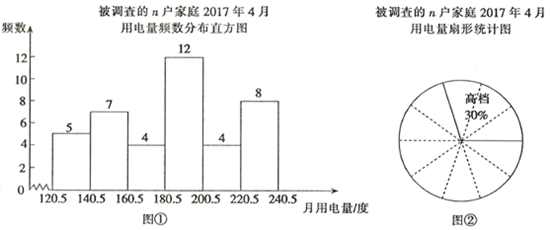
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com