
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点并与
两点并与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.
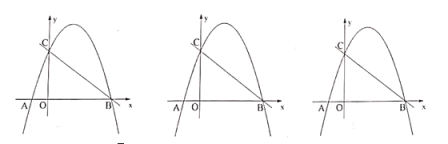
(1)求抛物线的解析式;
(2)点![]() 为直线
为直线![]() 上方对称轴右侧抛物线上一点,当
上方对称轴右侧抛物线上一点,当![]() 的面积为
的面积为![]() 时,求
时,求![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,连接![]() ,作
,作![]() 轴于
轴于![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 为线段
为线段![]() 上一点,点
上一点,点![]() 为线段
为线段![]() 上一点,满足
上一点,满足![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)R(3,3);(3)1或
;(2)R(3,3);(3)1或![]() .
.
【解析】
(1)求出A、B、C的坐标,把A、B的坐标代入抛物线解析式,解方程组即可得出结论;
(2)设R(t,![]() ).作RK⊥y轴于K,RW⊥x轴于W,连接OR.
).作RK⊥y轴于K,RW⊥x轴于W,连接OR.
根据![]() 计算即可;
计算即可;
(3)在RH上截取RM=OA,连接CM、AM,AM交PE于G,作QF⊥OB于H.分两种情况讨论:①点E在F的左边;②点E在F的右边.
(1)当x=0时y=3,
∴C(0,3),
∴OC=3.
∵OC=3OA,
∴OA=1,
∴A(-1,0).
当y=0时x=4,
∴B(4,0).
把A、B坐标代入得![]() 解得:
解得: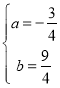 ,
,
∴抛物线的解析式为![]() .
.
(2)设R(t,![]() ).
).
作RK⊥y轴于K,RW⊥x轴于W,连接OR.

∵![]()
![]()
∵![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),![]() ,
,
∴R(3,3).
(3)在RH上截取RM=OA,连接CM、AM,AM交PE于G,作QF⊥OB于H.
分两种情况讨论:①当点E在F的左边时,如图1.
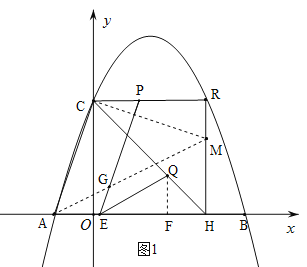
∵CR=CO,∠CRM=∠COA,
∴△CRM≌△COA,
∴CM=CA,∠RCM=∠OCA,
∴∠ACM=∠OCR=90°,
∴∠CAM=∠CMA=45°.
∵AC∥PE,
∴∠CAM=∠AGE=45°.
∵∠PEQ=45°,
∴∠AGE=∠PEQ,
∴AM∥EQ,
∴∠MAH=∠QEF.
∵∠QFE=∠MHA=90°,
∴△QEF∽△MAH,
∴![]() .
.
∵OA=1,OH=3,MH=RH-RM=3-1=2,
∴AH=AO+OH=4,
∴EF=2QF.
设CP=m,
∴QH=![]() CP=
CP=![]() m.
m.
∵OC=OH,
∴∠OHC=45°,
∴QF=FH=m,
∴EF=2m,
∴EH=3m.
∵ACPE为平行四边形,
∴AE=CP=m.
∵EH=AH-AE=4-m,
∴3m=4-m,
∴m=1,
∴CP=1.
②当点E在F的右边时,设AM交QE于N.如图2.

∵CR=CO,∠CRM=∠COA,
∴△CRM≌△COA,
∴CM=CA,∠RCM=∠OCA,
∴∠ACM=∠OCR=90°,
∴∠CAM=∠CMA=45°.
∵AC∥PE,
∴∠CAM=∠AGE=45°.
∵∠PEQ=45°,
∴∠AGE=∠PEQ=45°,
∴∠ENG=∠ENA=90°.
∵∠EQF+∠QEF=90°,∠EAN+∠QEF=90°,
∴∠EQF=∠MAB.
∵∠QFE=∠AHM=90°,
∴△QEF∽△AMH,
∴![]() ,
,
∴QF=2EF.
设CP=m,
∴QH=![]() CP=
CP=![]() m.
m.
∵OC=OH,
∴∠OHC=45°,
∴QF=FH=m,
∴EF=![]() m,
m,
∴EH=![]() m.
m.
∵ACPE为平行四边形,
∴AE=CP=m.
∵EH=AH-AE=4-m,
∴4-m=![]() m,
m,
∴m=![]() ,
,
∴CP=![]() .
.
综上所述:CP的值为1或![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】将正面分别写着数字![]() ,1,3,6的四张卡片(卡片除数字外,其它都相同)洗匀后,背面向上放在桌子上,从中先随机抽取一张卡片,记下卡片上的数字,不放回,再从中任取一张卡片,记下数字.
,1,3,6的四张卡片(卡片除数字外,其它都相同)洗匀后,背面向上放在桌子上,从中先随机抽取一张卡片,记下卡片上的数字,不放回,再从中任取一张卡片,记下数字.
(1)请用列表或画树状图法(树状图也称树形图)中的一种方法,列出所有可能出现的结果;
(2)请计算两次摸出的卡片上的数字之和大于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
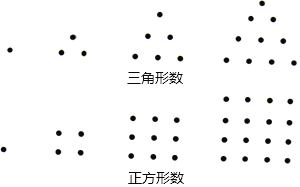
A. 33 B. 301 C. 386 D. 571
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD中,AB=5,BC=3,E为AD上一点,把矩形ABCD沿BE折叠,若点A恰好落在CD上点F处,则AE的长为_____.
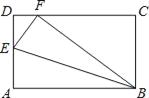
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
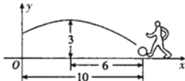
(1)如图建立直角坐标系,当球飞行的路线为一抛物线时,求此抛物线的解析式.
(2)已知球门高为2.44米,问此球能否射中球门(不计其它情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(m+1)x﹣m﹣2(m>0)与x轴交于A、B两点,与y轴交于点C,不论m取何正数,经过A、B、C三点的⊙P恒过y轴上的一个定点,则该定点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,龙岗区家庭轿车的拥有量逐年增加.据统计,某小区2017年底拥有家庭轿车81辆,2019年底家庭轿车的拥有量达到144辆.
(1)若该小区2017年底到2019年底家庭轿车拥有量的年平均增长率都相同,求该小区到2020年底家庭轿车将达到多少辆?
(2)为了缓解停车矛盾,该小区决定投资25万元再建造若干个停车位.据测算,建造费用分别为室内车位6000元/个,露天车位2000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的3倍,但不超过室内车位的4.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次用频率估计概率的试验中,统计了某一结果出现的频率,给出的 统计图如图所示,则符合这一结果的试验可能是 ( )
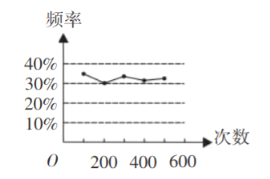
A.掷一枚硬币,出现正面朝上的概率
B.掷一枚硬币,出现反面朝上的概率
C.掷一枚骰子,出现 ![]() 点的概率
点的概率
D.从只有颜色不同的两个红球和一个黄球中,随机取出一个球是黄球的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com