
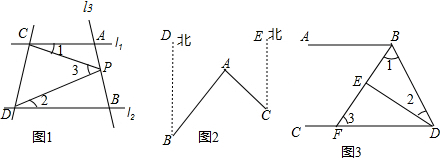
分析 (1)在图1中,作PM∥AC,利用平行线性质即可证明;利用①结论即可求得∠BAC的度数.
(2)根据BE、DE平分∠ABD、∠BDC,且∠1+∠2=90°,可得∠ABD+∠BDC=180°,根据同旁内角互补,可得两直线平行.根据∠1+∠2=90°,即∠BED=90°;那么∠3+∠FDE=90°,将等角代换,即可得出∠3与∠2的数量关系.
解答 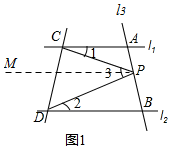 解:(1)如图1中,作PM∥AC,
解:(1)如图1中,作PM∥AC,
∵AC∥BD,
∴PM∥BD,
∴∠1=∠CPM,∠2=∠MPD,
∴∠1+∠2=∠CPM+∠MPD=∠CPD=∠3.
由题可知:∠BAC=∠B+∠C,
∵∠B=40°,∠C=45°,
∴∠BAC=40°+45°=85°.
故答案为:∠1+∠2=∠3,85°.
(2)证明:∵BE、DE平分∠ABD、∠BDC,
∴∠1=$\frac{1}{2}$∠ABD,∠2=$\frac{1}{2}$∠BDC;
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°;
∴AB∥CD;(同旁内角互补,两直线平行)
∵DE平分∠BDC,
∴∠2=∠FDE;
∵∠1+∠2=90°,
∴∠BED=∠DEF=90°;
∴∠3+∠FDE=90°;
∴∠2+∠3=90°.
点评 此题主要考查了角平分线的性质以及平行线的判定,正确添加辅助线是解决问题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | 当AB=BC时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当∠ABC=90°时,它是矩形 | D. | 当AC=BD时,它是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0米 | B. | 0.2米 | C. | -0.8米 | D. | -0.2米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某区中小学生视力情况 | B. | 了解七(2)班学生校服的尺码情况 | ||
| C. | 检测一批炮弹的使用寿命 | D. | 调查《1818黄金眼》栏目的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com