
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,交AD于F,FG∥BC,FH∥AC,下列结论:①AE=AF;②AF=FH;③AG=CE;④AB+FG=BC,其中正确的结论有 . (填序号)
【答案】①②③④
【解析】①正确.
∵∠BAC=90°
∴∠ABE+∠AEB=90°
∴∠ABE=90°-∠AEB
∵AD⊥BC
∴∠ADB=90°
∴∠DBE+∠BFD=90°
∴∠DBE=90-∠BFD
∵∠BFD=∠AFE
∴∠DBE=90°-∠AFE
∵BE平分∠ABC
∴∠ABE=∠DBE
∴90°-∠AEB=90°-∠AFE
∴∠AEB=∠AFE
∴AE=AF
②正确.
∵∠BAC=90°
∴∠BAF+∠DAC=90°
∴∠BAF=90°-∠DAC
∵AD⊥BC
∴∠ADC=90°
∴∠C+∠DAC=90°
∴∠C=90°-∠DAC
∴∠C=∠BAF
∵FH∥AC
∴∠C=∠BHF
∴∠BAF=∠BHF
在△ABF和△HBF中
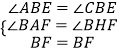
∴△ABF≌△HBF
∴AF=FH
③正确.
∵AE=AF,AF=FH
∴AE=FH
∵FG∥BC,FH∥AC
∴四边形FHCG是平行四边形
∴FH=GC
∴AE=GC
∴AE+EG=GC+EG
∴AG=CE
④正确.
∵四边形FHCG是平行四边形
∴FG=HC
∵△ABF≌△HBF
∴AB=HB
∴AB+FG=HB+HC=BC
故正确的答案有①②③④.
①根据直角三角形两锐角互余得出∠ABE=90°-∠AEB ,∠DBE=90-∠BFD ,根据对顶角相等及等量代换得出∠DBE=90°-∠AFE ,根据角平分线的定义得出∠ABE=∠DBE ,从而得出∠AEB=∠AFE ,根据等边对等角得出AE=AF ; ② 根据垂直的定义得出∠BAF=90°-∠DAC ,根据直角三角形两锐角互余得出∠C=90°-∠DAC ,根据同角的余角相等得出∠C=∠BAF ,根据平行线的性质得出∠C=∠BHF ,从而得出∠BAF=∠BHF ,然后利用AAS判断出△ABF≌△HBF ,根据全等三角形的性质得出AF=FH ; ③ 由 AE=AF,AF=FH得出 AE=FH ,利用两组对边分别平行得四边形是平行四边形得出 四边形FHCG是平行四边形 ,根据平行四边形的性质得出FH=GC ,进而得出AE=GC ,根据等式的性质得出AG=CE ;④根据平行四边形的性质得出FG=HC ,根据三角形全等得出AB=HB ,根据等式的性质得出AB+FG=HB+HC=BC 。


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
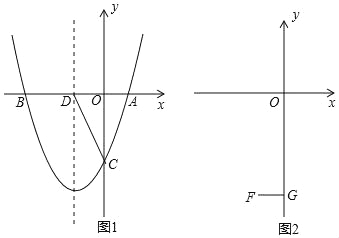
(1)若m=﹣3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE=![]() S△ACD,求点E的坐标;
S△ACD,求点E的坐标;
(3)如图2,设F(﹣1,﹣4),FG⊥y于G,在线段OG上是否存在点P,使∠OBP=∠FPG?若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )
A.∠1=∠2+∠A
B.∠1=2∠A+∠2
C.∠1=2∠2+2∠A
D.2∠1=∠2+∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一周时间有604800秒,数604800用科学记数法表示为( )
A.60.48×104B.6.048×106C.6.048×105D.0.6048×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com