
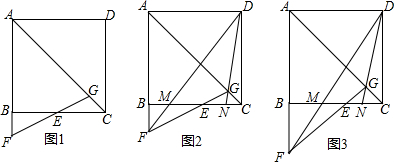
分析 (1)延长FG交CD于M,根据△BFE∽△CME,得到$\frac{BF}{CM}$=$\frac{BE}{CE}$,再根据△CMG∽△AFG,即可得到$\frac{CG}{AG}$=$\frac{CM}{AF}$=$\frac{BF}{AF}$=$\frac{1}{5}$;
(2)延长FG交CD于H,根据AB∥CD,CH=BF,可得$\frac{BF}{AF}$=$\frac{CG}{AG}$,再根据AD∥BM,AD∥CN,即可得出$\frac{BM}{AD}$=$\frac{CN}{AD}$,进而得到BM=CN;
(3)先根据△AFG、△BEF都是等腰直角三角形,得出BE=BF=$\frac{1}{2}$BC=2,AF=4+2=6,AG=$\frac{\sqrt{2}}{2}$AF=3$\sqrt{2}$,再根据$\frac{CN}{AD}$=$\frac{1}{3}$,可得CN=$\frac{4}{3}$,最后作GK⊥BC于K,则△CGK为等腰直角三角形,根据GK=$\frac{\sqrt{2}}{2}$CG=1,即可得出S△CNG=$\frac{1}{2}$CN×GK=$\frac{2}{3}$.
解答 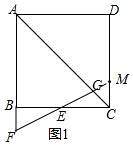 解:(1)CG:AG=1:5.
解:(1)CG:AG=1:5.
理由:如图1,延长FG交CD于M,
∵AB=4BF,
∴$\frac{BF}{AF}$=$\frac{1}{5}$,
∵BF∥CM,
∴△BFE∽△CME,
∴$\frac{BF}{CM}$=$\frac{BE}{CE}$,
又∵点E是BC的中点,
∴BF=CM,
∵AF∥CM,
∴△CMG∽△AFG,
∴$\frac{CG}{AG}$=$\frac{CM}{AF}$=$\frac{BF}{AF}$=$\frac{1}{5}$,
故答案为:$\frac{1}{5}$;
(2)证明:如图2,延长FG交CD于H,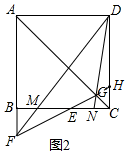
∵AB∥CD,
∴$\frac{CH}{AF}$=$\frac{CG}{AG}$,
由(1)可得,CH=BF,
∴$\frac{BF}{AF}$=$\frac{CG}{AG}$,
∵AD∥BM,AD∥CN,
∴$\frac{BF}{AF}$=$\frac{BM}{AD}$,$\frac{CG}{AG}$=$\frac{CN}{AD}$,
∴$\frac{BM}{AD}$=$\frac{CN}{AD}$,
∴BM=CN;
(3)S△CNG=$\frac{2}{3}$.
理由:∵FG⊥AC,∠FAG=45°,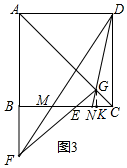
∴∠AFG=45°=∠BEF,
∴△AFG、△BEF都是等腰直角三角形,
∴BE=BF=$\frac{1}{2}$BC=2,
∴AF=4+2=6,AG=$\frac{\sqrt{2}}{2}$AF=3$\sqrt{2}$,
又∵AC=$\sqrt{2}$AB=4$\sqrt{2}$,
∴CG=AC-AG=$\sqrt{2}$,
∴$\frac{CG}{AG}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$,
∴$\frac{CN}{AD}$=$\frac{1}{3}$,即$\frac{CN}{4}$=$\frac{1}{3}$,
∴CN=$\frac{4}{3}$,
如图3,作GK⊥BC于K,则△CGK为等腰直角三角形,
∴GK=$\frac{\sqrt{2}}{2}$CG=$\frac{\sqrt{2}}{2}$×$\sqrt{2}$=1,
∴S△CNG=$\frac{1}{2}$CN×GK=$\frac{1}{2}$×$\frac{4}{3}$×1=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题属于四边形综合题,主要考查了相似三角形的判定与性质,平行线分线段成比例定理以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造相似三角形以及等腰直角三角形,依据相似三角形的对应边成比例进行推导计算.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
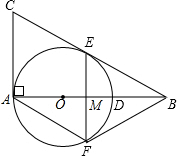 如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边AB相交于点D,与边BC相切于点E.
如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边AB相交于点D,与边BC相切于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
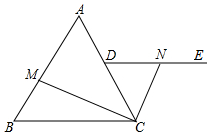 如图,在边长为6的等边△ABC中,D为AC中点,射线DE∥BC,M,N分别为线段AB与射线DE上的点,连结CM,CN,若BM=DN,则CM+CN的最小值为3$\sqrt{7}$.
如图,在边长为6的等边△ABC中,D为AC中点,射线DE∥BC,M,N分别为线段AB与射线DE上的点,连结CM,CN,若BM=DN,则CM+CN的最小值为3$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,对角线AC,BD交于点O,现有一块足够大的直角三角板的直角顶点与点O重合,当直角三角板绕着点O旋转时,两条直角边OP、OQ分别保持与边AB、边BC相交于点E、F,连结EF,下列结论:①EF=OB,②EF=$\sqrt{2}$OF;③当EF∥AC时,△BEF的周长最小;④当BE变化时,四边形OEBF的面积也随之变化.其中结论正确的个数为( )
如图,在正方形ABCD中,对角线AC,BD交于点O,现有一块足够大的直角三角板的直角顶点与点O重合,当直角三角板绕着点O旋转时,两条直角边OP、OQ分别保持与边AB、边BC相交于点E、F,连结EF,下列结论:①EF=OB,②EF=$\sqrt{2}$OF;③当EF∥AC时,△BEF的周长最小;④当BE变化时,四边形OEBF的面积也随之变化.其中结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,AE=DE,AC与BD相交于点E,∠ADB=60°,且BE:ED=3:1,BD=12,求梯形ABCD的周长.
如图,在梯形ABCD中,AD∥BC,AE=DE,AC与BD相交于点E,∠ADB=60°,且BE:ED=3:1,BD=12,求梯形ABCD的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com