
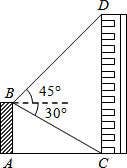
 如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(结果保留整数,参考值:$\sqrt{3}$≈1.732)
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(结果保留整数,参考值:$\sqrt{3}$≈1.732) 分析 作BE⊥CD于E.在Rt△CBE中,tan∠BCE=$\frac{BE}{CE}$,可得BE=CE•tan60°=12$\sqrt{3}$,在Rt△BDE中,由∠DBE=45°,可得DE=BE=12$\sqrt{3}$,根据CD=CE+DE计算即可.
解答 解:作BE⊥CD于E.
∵∠DBE=45°,∠CBE=30°,∠BCE=60°,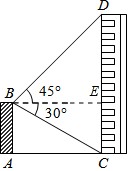
又∵AB⊥AC,CD⊥AC,
∴四边形ABEC是矩形,
∴CE=AB=12,
在Rt△CBE中,tan∠BCE=$\frac{BE}{CE}$,
∴BE=CE•tan60°=12$\sqrt{3}$,
在Rt△BDE中,∵∠DBE=45°,
∴DE=BE=12$\sqrt{3}$,
∴CD=CE+DE=12+12$\sqrt{3}$=12(1+$\sqrt{3}$)≈33m,
答:楼房CD的高度约为33m.
点评 本题考查解直角三角形-仰角俯角、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于基础题,中考常考题型.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
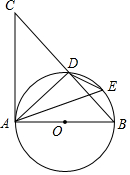 如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是$\widehat{BD}$上一点.
如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是$\widehat{BD}$上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
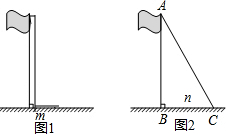 如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长m,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n,利用所学知识就能求出旗杆的长,若m=2,n=6,求旗杆AB的长.
如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长m,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n,利用所学知识就能求出旗杆的长,若m=2,n=6,求旗杆AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
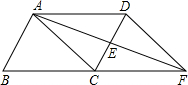 如图,在?ABCD中,E是CD的中点,AE是延长线交BC的延长线于F,分别连接AC,DF,解答下列问题:
如图,在?ABCD中,E是CD的中点,AE是延长线交BC的延长线于F,分别连接AC,DF,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com