
分析 (1)根据甲乙两种出租车的计价方式分别列式计算即可得解;
(2)都分x≤3和x>3两种情况列式表示即可;
(3)将x=14分别代入代数式计算即可得解.
解答 解:(1)当x=5时,甲的费用=10+(5-3)×1.2=10+2.4=12.4(元),
乙的费用=8+(5-3)×1.8=8+3.6=11.6(元),
答:乘坐甲、乙两种出租车的费用分别为12.4元,11.6元;
(2)甲的费用$\left\{\begin{array}{l}{10(x≤3)}\\{10+1.2(x-3)(x>3)}\end{array}\right.$,
乙的费用$\left\{\begin{array}{l}{8(x≤3)}\\{8+1.8(x-3)(x>3)}\end{array}\right.$;
(3)∵此人乘坐的路程为13千米多一点,
∴x=14,
甲的费用10+1.2(14-3)=10+13.2=23.2(元),
乙的费用8+1.8(14-3)=8+19.8=27.8(元),
∵23.2<27.8,
∴他乘坐甲出租车更合算.
点评 本题考查了代数式求值,读懂题目信息,理解两种出租车的计价方式并准确列出算式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
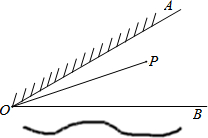 如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.
如图,∠AOB=30°,OA表示草地边,OB表示河边,点P表示家且在∠AOB内.某人要从家里出发先到草地边给马喂草,然后到河边喂水,最后回到家里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
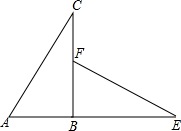 如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:
如图,△ABC是直角三角形,延长AB到点E,使BE=BC,在BC上取一点F,使BF=AB,连接EF,△ABC旋转后能与△FBE重合,请回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com