
 如图,在平面直角坐标系中,OB=OA=6,OC=12,点P从A出发运动到C点,将BP绕P顺时针旋转90°得到点Q,求在整个运动的过程中,Q点滑过的长度为6$\sqrt{2}$.
如图,在平面直角坐标系中,OB=OA=6,OC=12,点P从A出发运动到C点,将BP绕P顺时针旋转90°得到点Q,求在整个运动的过程中,Q点滑过的长度为6$\sqrt{2}$. 分析 如图连接PB、BQ、PQ,作QH⊥x轴于H,首先证明∠QAH=45°,设点P与A重合时,点Q在Q′处,点P与C重合时,点Q在Q″处,推出点Q的运动轨迹是线段Q′Q″.
解答 解:如图连接PB、BQ、PQ,作QH⊥x轴于H.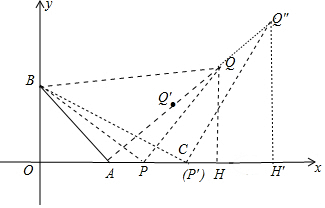
∵PB=PQ,∠BPQ=90°,
∴∠BPO+∠OBP=90°,∠OPB+∠QPH=90°,
∴∠OBP=∠HPQ,∵∠POB=∠QHP=90°,
∴△OPB≌△HQP,
∴OB=PB=OA=6,OP=QH,
∵OP=6+OP,AH=AP+6,
∴OP=AH=QH,
∴∠QAH=45°,
设点P与A重合时,点Q在Q′处,点P与C重合时,点Q在Q″处.
∴点Q的运动轨迹是线段Q′Q″.
当点P与C重合时,P′B=$\sqrt{O{B}^{2}+O{C}^{2}}$=6$\sqrt{5}$,AH′=H′Q′′=12,
∴AQ″=$\sqrt{2}$QH=12$\sqrt{2}$,∵AQ′=AB=6$\sqrt{2}$,
∴Q′Q″=12$\sqrt{2}$-6$\sqrt{2}$=6$\sqrt{2}$,
故答案为6$\sqrt{2}$.
点评 本题考查了坐标与图形变化-旋转,等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找点Q的运动轨迹,学会添加常用辅助线,构造全等三角形解决问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
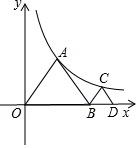 如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).
如图,等边△OAB和等边△BCD的顶点A、C分别在双曲线y=$\frac{k}{x}$的图象上,若OA=1,则点C的坐标为($\frac{\sqrt{2}+1}{2}$,$\frac{\sqrt{6}-\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
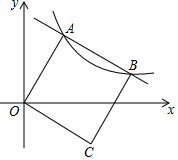 如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,2) | B. | (-3,-2) | C. | (-2,-3) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com