
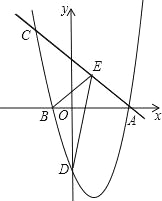
【题目】如图,抛物线y=![]() +bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
+bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标.
【答案】(1) y=![]() ﹣3x﹣4;(2) E(
﹣3x﹣4;(2) E(![]() ,
,![]() ).
).
【解析】
试题分析:(1)直接把点A(4,0),B(﹣1,0)代入抛物线y=![]() +bx﹣4求出a、b的值,进而可得出抛物线的解析式;
+bx﹣4求出a、b的值,进而可得出抛物线的解析式;
(2)先判断出周长最小时BE⊥AC,即作点B关于直线AC的对称点F,连接DF,交AC于点E,联立方程组即可.
试题解析:(1)∵抛物线y=![]() +bx﹣4与x轴交于两点A(4,0),B(﹣1,0),
+bx﹣4与x轴交于两点A(4,0),B(﹣1,0),
∴![]() ,解得
,解得![]() ,
,
∴此抛物线的解析式为:y=![]() ﹣3x﹣4;
﹣3x﹣4;
(2)如图1,作点B关于直线AC的对称点F,连接DF交AC于点E,
由(1)得,抛物线解析式为y=![]() ﹣3x﹣4,
﹣3x﹣4,
∴D(0,﹣4),
∵直线y=﹣x+4交抛物线于点C,
∴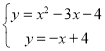 ,解得,
,解得,![]() 或
或![]() ,
,
∴C(﹣2,6),
∵A(4,0),
∵直线AC解析式为y=﹣x+4,直线BF⊥AC,且B(﹣1,0),
∴直线BF解析式为y=x+1,
设点F(m,m+1),
∴G(![]() ,
,![]() ),
),
∵点G在直线AC上,
∴![]() +4=
+4=![]() ,
,
∴m=4,
∴F(4,5),
∵D(0,﹣4),
∴直线DF解析式为y=![]() x﹣4,
x﹣4,
解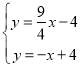 得
得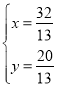 ,
,
∴直线DF和直线AC的交点E(![]() ,
,![]() ).
).



科目:初中数学 来源: 题型:
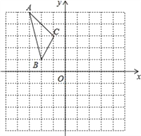
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是运动员.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
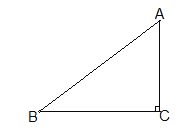
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).
(1)若点P在BC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小学,我们已经初步了解到,长方形的对边平行且相等,每个角都是90°.如图,长方形ABCD中,AD=9cm,AB=4cm,E为边AD上一动点,从点D出发,以1cm/s向终点A运动,同时动点P从点B出发,以acm/s向终点C运动,运动的时间为ts.
(1)当t=3时,
①求线段CE的长;
②当EP平分∠AEC时,求a的值;
(2)若a=1,且△CEP是以CE为腰的等腰三角形,求t的值;
(3)连接DP,直接写出点C与点E关于DP对称时的a与t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
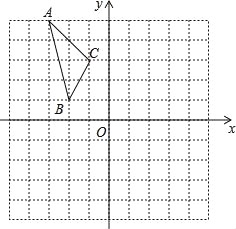
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到![]() ,已知点
,已知点![]() 的坐标为(4,0),写出顶点
的坐标为(4,0),写出顶点![]() ,
,![]() 的坐标;
的坐标;
(2)若△ABC和![]() 关于原点O成中心对称图形,写出
关于原点O成中心对称图形,写出![]() 的各顶点的坐标;
的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到![]() ,写出
,写出![]() 的各顶点的坐标.
的各顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com